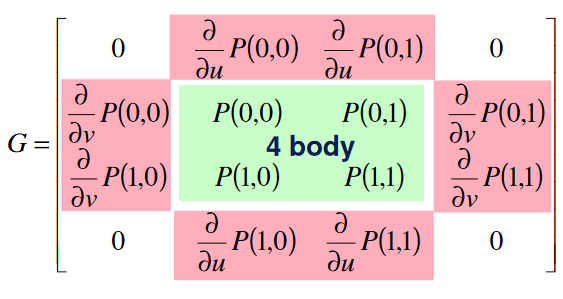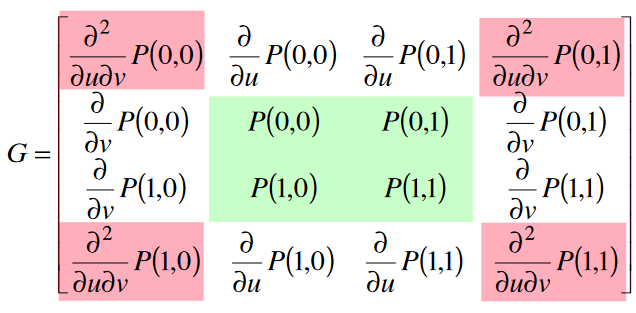23 KiB
| title | description |
|---|---|
| Křivky a povrchy | TODO |
Note
Implicitní a parametrické reprezentace. Interpolace a aproximace. Cn, Gn spojitost, podmínky spojitosti pro po částech definované funkce. Bézierovy křivky, B-spline křivky, ~NURBS,~ Coonsovy ~křivky a~ pláty. Povrchy tvořené rekurzivním dělením polygonů.
PB009, PA010
Druhy reprezentace
Jak povrchy tak křivky mohou být reprezentovány třemi způsoby:
Explicitní reprezentace
Křivka nebo povrch je vyjádřen pomocí funkce.
\begin{align*}
y &= f(x) & \text{ pro křivku} \\
z &= f(x, y) & \text{ pro povrch}
\end{align*}
Omezení na funkce je však příliš silné. Spoustu pěkných křivek a povrchů nelze vyjádřit pomocí jediné funkce.
Implicitní reprezentace
Máme k dispozici rovnici ve tvaru:
\begin{align*}
F(x, y) &= c & \text{ pro křivku} \\
F(x, y, z) &= c & \text{ pro povrch}
\end{align*}
kde c je konstanta a je obvykle rovná 0.
Tato rovnice udává množinu bodů, ze které se křivka nebo povrch sestává. Takové množině se někdy říká level set a metodám, které s nimi pracují level-set methods.
Important
Výhodou implicitně zadaných ploch je kompaktnější reprezentace a jednodušší ray casting. Nicméně výpočty s nimi jsou časově náročné, takže se stejně nejdřív převádí na polygonové meshe -- polygonizace.
Important
Tahle sekce přesahuje do 3D modelování a datové struktury -> Implicitní reprezentace a modelování.
Parametrická reprezentace
Udává dráhu pohybujícího se bodu, či něco jako hladinu povrchu. Snadno se z ní vyjadřuje tečna, čehož se využívá při jejich skládání.
Pro křivky:
\begin{align*}
Q(t) &= \lbrack x(t), y(t), z(t) \rbrack & \text{ (bodová rovnice křivky)} \\
\vec{q}(t) &= (x(t), y(t), z(t)) & \text{ (vektorová rovnice křivky)}
\end{align*}
kde t je "čas" z intervalu \lbrack t_\text{min}, t_\text{max} \rbrack, nejčastěji \lbrack 0, 1 \rbrack. Výhodné je, že takto zadaná křivka se může sama křížit, uzavírat, a podobně.
Analogicky pro povrchy:
Q(u, v) = \lbrack x(u, v), y(u, v), z(u, v) \rbrack
kde pro u a v už metafora s časem nefunguje. Obvykle obě náleží do intervalu \lbrack 0, 1 \rbrack.
Terminologie
Pro zbytek otázky je podstatné znát několik termínů:
-
Dotykový / tečný / tangent vektor křivky
Aktuální směr křivky v daném bodě. Z parametricky vyjádřené křivky\vec{q}ho lze v časet_0získat jako derivaci:\vec{q}'(t_0) = \left( \frac{\partial x(t_0)}{\partial t}, \frac{\partial y(t_0)}{\partial t}, \frac{\partial z(t_0)}{\partial t} \right)Rovnice tečny
\vec{p}je pak\vec{p}(u) = \vec{q}(t_0) + \vec{q}'(t_0) \cdot u. -
Polynomiální křivka
Velmi častý druh křivek v počítačové grafice. Vypadají jako:Q_n(t) = a_0 + a_1 \cdot t + a_2 \cdot t^2 + \ldots + a_n \cdot t^nJe velmi snadné je evaluovat a derivovat. Z nich často skládáme křivky po částech.
-
Kubika
Polynomiální křivka třetího stupně.Parametricky:
\begin{align*} x(t) = a_{x}t^{3} + b_{x}t^{2} + c_{x}t + d_{x} \\ y(t) = a_{y}t^{3} + b_{y}t^{2} + c_{y}t + d_{y} \\ z(t) = a_{z}t^{3} + b_{z}t^{2} + c_{z}t + d_{z} \end{align*}Zapsáno pomocí matice:
Q(t) = T \cdot C = \lbrack t^3, t^2, t, 1 \rbrack \cdot \begin{bmatrix} a_x & a_y & a_z \\ b_x & b_y & b_z \\ c_x & c_y & c_z \\ d_x & d_y & d_z \end{bmatrix}Tečný vektor
\vec{q'}je pak:\vec{q'}(t) = \frac{\partial}{\partial t} \cdot C = \lbrack 3t^2, 2t, 1, 0 \rbrack \cdot CU kubik platí, že
C = M \cdot G, kdeMje bázová matice aGje vektor geometrických podmínek.T \cdot Mdefinuje polynomiální bázi -- skupinu polynomů -- která je společná pro všechny křivky určitého typu.Gpak obsahuje parametry konkrétní křivky -- řídící a dotykové body.tudává, jestli jsme na začátku či konci křivky.
-
Tečná rovina
Rovina, která se povrchu dotýká v konkrétním bodě a její normála je na povrch kolmá. Pro parametrickou plochuQje tečná plochaTdána jako:\begin{align*} \vec{q_{u}}(u,v) &= \frac{\partial Q(u,v)}{\partial u} = \left( \frac{\partial x(u,v)}{\partial u}, \frac{\partial y(u,v)}{\partial u}, {\partial z(u,v) \over \partial u} \right) \\ \vec{q_{v}}(u,v) &= \frac{\partial Q(u,v)}{\partial v} = \left( \frac{\partial x(u,v)}{\partial v}, \frac{\partial y(u,v)}{\partial v}, {\partial z(u,v) \over \partial v} \right) \\ T(r,s) &= Q(u,v) + r.\vec{q_{u}} + s.\vec{q_{v}}, \quad r,s \in \mathbb{R} \end{align*}kde
\vec{q_u}je tečný vektor ve směru parametruu, a analogicky\vec{q_v} -
Normála / kolmice
Normálu\vec{n}parametricky dané plochyQurčíme jako vektorový součin tečných vektorů:\vec{n} = \frac{\vec{q_u} \times \vec{q_v}}{\left\lVert \vec{q_u} \times \vec{q_v} \right\rVert} -
Gradient
Funkce, která vrací "směr a velikost největšího růstu". Nejčastěji se používá u povrchů k určení normály, ale lze ji použít v libovolné dimenzi k různým účelům. Pokud je povrchfzadán implicitně, pak je gradient:\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)
Interpolace a aproximace
-
Interpolace
Prokládání daných bodů křivkou. Konstrukce křivky, která interpolovanými body prochází.V případě kubiky výše to znamená, že
Gobsahuje body, kterými křivka prochází.Mějmě funkci
f(x), jejíž hodnotu známe v bodechf(x_0), f(x_1), \ldots, f(x_n). Interpolace znamená nalezení hodnotf(x)pro všechnax_0 < x < x_n. -
Aproximace
Přiblížení, odhad. Je nepřesným popisem nějaké jiné entity (např. čísla či funkce). Saháme k ní, pokud pro analytické řešení nemáme dost informací nebo výpočetní kapacity. Aproximace je méně přesná než interpolace, ale výpočetně jednodušší.V případě kubiky výše to znamená, že
Gobsahuje řídící body, které sice udávají směr křivky, ale ta jimi neprochází.
Spojitost
Představme si, že máme dva segmenty křivky: Q_1 a Q_2, spojené v bodě t, tedy Q_1(t) = Q_2(t). Tento bod nazýváme uzlem (knot). Spojitost je zjednodušeně způsob, jakým jsou tyhle segmenty spojeny v uzlu.
Parametrická spojitost stupně n (C^n)
Křivka Q patří do třídy C^n, pokud má ve všech bodech t spojitou derivaci až do řádu n.
-
C^0-- dva segmenty jsou spojené; konečný bod jednoho segmentu je počátečním bodem druhého. -
C^1-- platíC^0a navíc je tečný vektor na konci prvního segmentu shodný s tečným vektorem na začátku druhého segmentu -- první derivace v uzlu jsou si rovny. -
C^2-- platíC^1a druhé derivace v uzlu jsou si rovny. -
C^n-- platíC^{n-1}a navíc jsou si $n$-té derivace v uzlu rovny. -
Bod pohybující se po $C^0$-spojité dráze sebou "trhne" v prostoru, když projde uzlem.
-
V případě
C^1křivky se při průchodu uzlem směr ani rychlost prudce nezmění, může se však změnit zrychlení. -
V případě
C^2křivky se při průchodu uzlem nezmění už ani zrychlení.
Geometrická spojitost stupně n (G^n)
Je podobná parametrické spojitosti, ale vyžaduje jen "geometrickou" spojitost. Vyžaduje, aby si derivace byly sobě úměrné. 1 2
G^0-- koncový bod prvního segmentu je totožný s počátečním bodem druhého segmentu (C^0 = G^0).G^1-- platíG^0a navíc je směr tečny na konci prvního segmentu shodný s směrem tečny na začátku druhého segmentu. Velikost tečného vektoru (rychlost) se však může prudce změnit.G^2-- platíG^1a navíc mají stejný střed křivosti (center of curvature). 3
Platí, že C^n \Rightarrow G^n, ale obráceně G^n \not\Rightarrow C^n.
Note
Podle slidů z PB009 musí faktor úměrnosti být různý od 0. 4 Podle Barskyho a DeRoseho musí v první derivaci být
> 0a v dalších už je to šumák. 2 Co je správně? Kdo ví. Nemám dost častu to zjistit, takže to ponechávám jako cvičení čtenáři.
Křivky
Lagrangeův interpolační polynom
Základní metoda interpolace funkce, jejíž hodnotu známe jen v n + 1 diskrétních bodech P_0, P_1, ... P_n. Sestává se z pomocných polynomů \ell_i: 5
\ell_i(x) = \prod_{0 \le k \le n, k \neq i}^n \frac{x - x_k}{x_i - x_k}
Který splňuje podmínku:
\ell_i(x_k) = \begin{cases}
1 & \text{ pro } i = k \\
0 & \text{ pro } i \neq k
\end{cases}
Pak polynom P interpoluje danou množinu bodů:
P(x) = \sum_{i=0}^n P_i \ell_i(x)
Blbé je, že musíme všechny pomocné polynomy přepočítat, když přidáme nový bod.
-
Hornerovo schéma / Horner's method
Metoda evaluace polynomů. Vychází z myšlenky, že násobení se dá nestovat: 6\begin{aligned} & a_0 + a_1 \cdot x + a_2 \cdot x^2 + ... + a_n \cdot x_n \\ & = a_0 + x(a_1 + x(a_2 + ... + x(a_{n-1} + x \cdot a_n)...)) \end{aligned}Vyžaduje jen
nnásobení ansčítání, což je optimální.
Hermitovské křivky
Asi nejznámnější interpolační křivky v počítačové grafice. Jsou určeny dvěma řídícími body -- P_0 a P_1 -- a dvěma dotykovými vektory -- \vec{p_0'} a \vec{p_1'}. Řídící body určují začátek a konec křivky, dotykové vektory její směr a vyklenutí. Pokud jsou oba vektory nulové, je to úsečka.
Je jednoduché je na sebe navázat v C^1, neboť tečné vektory jsou přímo součástí definice.
-
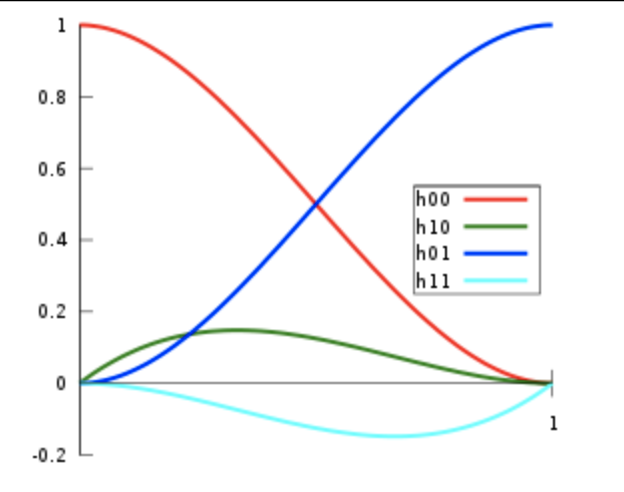
Cubic Hermite spline / Ferguson curve
Pro Hermitovskou kubiku platí: 7 8\begin{aligned} Q(t) &= \begin{bmatrix} t^{3} & t^{2} & t & 1 \end{bmatrix} \cdot \begin{bmatrix} 2 & -2 & 1 & 1 \\ -3 & 3 & -2 & -1 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} P_{0} \\ P_{1} \\ \vec{p'}_{0} \\ \vec{p'}_{1} \end{bmatrix} = \\ &= P_0 \cdot F_1(t) + P_1 \cdot F_2(t) + \vec{p'}_0 \cdot F_3(t) + \vec{p'}_1 \cdot F_4(t) \end{aligned}kde
F_1, F_2, F_3, F_4jsou Hermitovské polynomy 3. stupně:\begin{aligned} \textcolor{red}{F_1(t)} &= 2t^3 - 3t^2 + 1 \\ \textcolor{blue}{F_2(t)} &= -2t^3 + 3t^2 \\ \textcolor{green}{F_3(t)} &= t^3 - 2t^2 + t \\ \textcolor{cyan}{F_4(t)} &= t^3 - t^2 \end{aligned}
Bézierova křivka
Asi nejčastěji používaná aproximační křivka. Využívá se zejména ve 2D grafice, třeba při definici fontů.
- Bézierova křivka $n$-tého stupně je definována
n + 1řídícími bodyP_0, P_1, ... P_n. - Změnou polohy jednoho bodu dojde ke změně celé křivky. Proto se často dělí na segmenty menšího stupně, které se pak navazují na sebe.
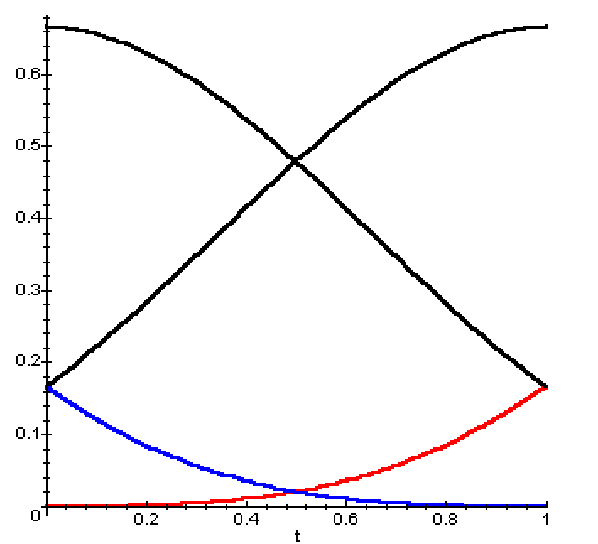
Základem jsou Bernsteinovy polynomy $n$-tého stupně:
[stem] b_{\nu,n}(x) = \binom{n}{\nu} x^{\nu} \left( 1 - x \right)^{n - \nu}, \quad \nu = 0, \ldots, n,
Mezi jejich vlastnosti patří:
- Nezápornost:
b_{\nu,n}(x) \ge 0prox \in \lbrack 0, 1 \rbrack. - Jejich součet je roven jedné:
\sum_{\nu = 0}^n b_{\nu,n}(x) = 1. - Dají se vyjádřit rekurzí:
b_{\nu,n}(x) = (1 - x) \cdot b_{\nu,n-1}(x) + x \cdot b_{\nu-1,n-1}(x).
Bernstein basis polynomials for 4th degree curve blending by VisorZ
-
DeCasteljau algorithm
Rekurzivní algoritmus pro konstrukci Bézierových křivek. Využívá vlastností Bernsteinových polynomů. -
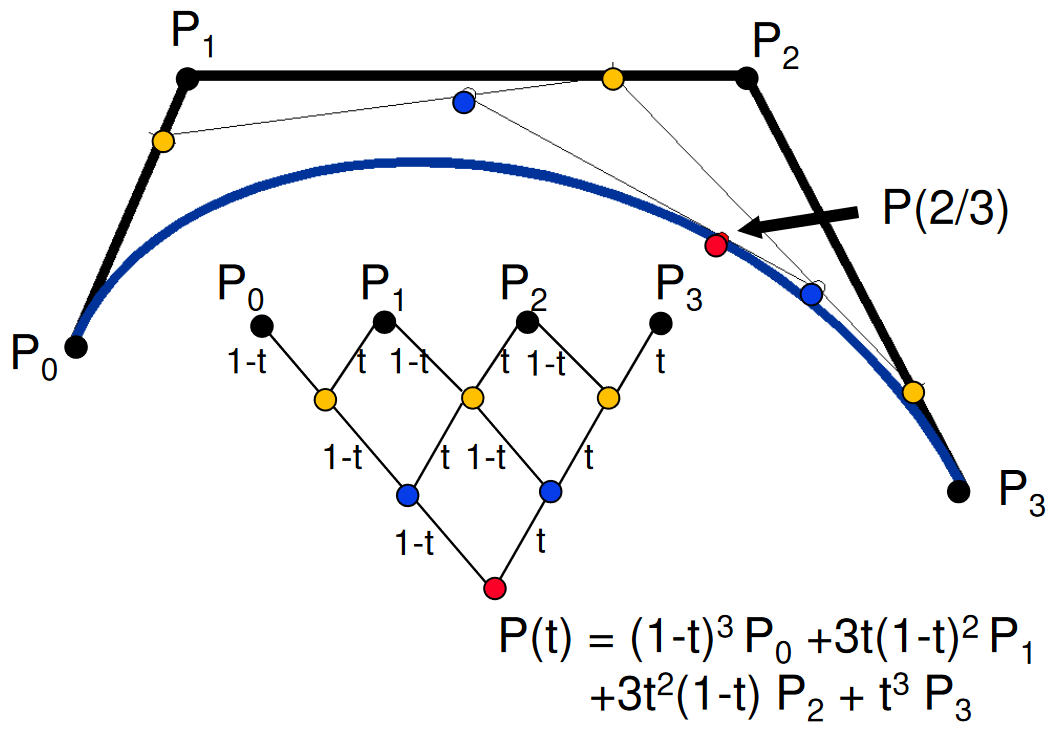
Bézierova kubika
Bézierova křivka třetího stupně. Je dána čtyřmi řídícími bodyP_0, P_1, P_2, P_3:P(t) = (1 - t)^3 \cdot P_0 + 3 \cdot (1 - t)^2 \cdot t \cdot P_1 + 3 \cdot (1 - t) \cdot t^2 \cdot P_2 + t^3 \cdot P_3
B-spline
-
Splajn / spline
Splajn stupněnpo částech definovaná polynomiální funkce stupněn-1proměnnéx. 9Po částech definovaná / piecewise znamená, že má několik intervalů a pro každý z nich jiný polynom.
- Místa, kde se části polynomu dotýkají jsou uzly a jsou značeny pomocí
t_0, t_1, ..., t_na řazeny v neklesajícím pořadí. - Pokud jsou uzly unikátní, pak je splajn v uzlech
C^{n-2}spojitý. 9 - Pokud je
ruzlů shodných, je v tomto místě pouzeC^{n-r-1}spojitý.
- Místa, kde se části polynomu dotýkají jsou uzly a jsou značeny pomocí
Basis spline / B-spline stupně n je aproximační křivka / splajn daná sekvencí n uzlů. Jako funkce vrací užitečné hodnoty jen mezi prvním a posledním uzlem, všude jinde je nulová. Svůj název dostala podle toho, že B-splajny slouží jako bázové funkce pro splajnové křivky.
Lze ji definovat pomocí Cox-de Boorovy rekurzivní formule:
Tip
de Boorův algoritmus je generalizací DeCasteljauova algoritmu ale pro B-splajny.
\begin{aligned}
B_{i,0}(x) &= \begin{cases}
1 & \text{pro } t_i \le x < t_{i+1} \\
0 & \text{jinak}
\end{cases}
\\
B_{i,n}(x) &= \textcolor{red}{\frac{x - t_i}{t_{i+n} - t_i}} B_{i,n-1}(x)
+ \textcolor{blue}{\frac{t_{i+n+1} - x}{t_{i+n+1} - t_{i+1}}} B_{i+1,n-1}(x)
\end{aligned}
Zatímco x jde od t_i k t_{i+n}, červený výraz začíná na 1 a klesá k 0.
Podobně, zatímco x jde od t_{i+1} k t_{i+n+1}, modrý výraz začíná na 0 a roste k 1.
Navíc platí \sum_{i=0}^{n} B_{i,n}(x) = 1.
Jejich užitečnost spočívá v tom, že libovolný splajn stupně n daný sekvencí uzlů lze vyjádřit jako lineární kombinaci B-splajnů:
S(x) = \sum_{i=0} c_i B_{i,n}(x)
Note
Uzlů je zpravidla víc než
n+1, protože pak teprve máme víc než jeden B-spline, který kombinujeme.
-
Uniformní B-splajny
Uzly jsou rozloženy rovnoměrně. Tedy mezi každými dvěma uzlyt_iat_{i+1}je stejná vzdálenosth.Příklad:
T = \begin{bmatrix} t_0 & t_1 & t_2 & t_3 \end{bmatrix} = \begin{bmatrix} 0 & 0.\overline{3} & 0.\overline{6} & 1 \end{bmatrix} -
Coonsova kubika
KubikaPdaná 4 řídícími bodyP_0, P_1, P_2, P_3. Neprochází ani jedním z kontrolních bodů. 10\begin{aligned} P(t) &= B_0(t) \cdot P_0 + B_1(t) \cdot P_1 + B_2(t) \cdot P_2 + B_3(t) \cdot P_3, t \in \lbrack 0, 1 \rbrack \\ B_0(t) &= \frac{1}{6} (1 - t)^3 \\ B_1(t) &= \frac{1}{6} (3t^3 - 6t^2 + 4) \\ B_2(t) &= \frac{1}{6} (-3t^3 + 3t^2 + 3t + 1) \\ B_3(t) &= \frac{1}{6} t^3 \end{aligned}Note
Něco ohledně tohohle termínu mi hrozně smrdí. Zdá se, že jediní, kdo používají "coons cubic curve" jsme my a ČVUT.
Povrchy
Interpolace je náročná, proto se častěji používají aproximační povrchy.
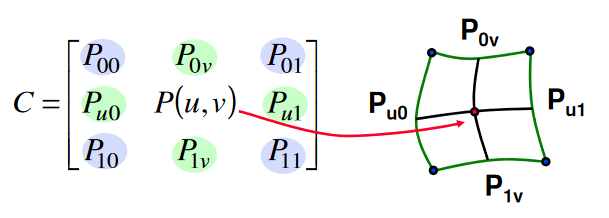
Interpolační plocha
Plocha \vec{P}.
Dáno:
(m + 1) \times (n + 1)řídících bodů\vec{P}_{i,j}.m + 1hodnotu_kan + 1hodnotv_l.
Platí, že \vec{P}(u_k, u_l) = \vec{P}_{k,l} pro k = 0, 1, ..., m a l = 0, 1, ..., n.
Interpolujeme vektorovým polynomem \vec{a}_{i,j}:
\vec{P}(u, v) = \sum_{i = 0}^m \sum{j = 0}^n \vec{a}_{i,j} \cdot u^i \cdot v^j
V případě Lagrangeova polynomu je \vec{a}_{i,j} = \ell_i^m(u) \cdot \ell_j^n(v).
Hermitovský plát
Interpolační povrch.
-
12-ti vektorová varianta
4 rohové body a 8 tečných vektorů. -
16-ti vektorová varianta
4 rohové body, 8 tečných vektorů a 4 zkrutové vektory.
Coonsovy pláty / Coonsovy plochy / Coons patch
Plochy vzniknuvší interpolací mezi křivkami udávající jejich okraje. Dají se na sebe pěkně napojovat, právě protože jsou definovány svými okraji.
Warning
Coonsovy pláty jsou interpolační, zatímco Coonsovy křivky jsou aproximační.
-
Bilineární Coonsovy pláty
Určeny 4 křivkami
P(u, 0), P(u, 1), P(0, v), P(1, v), které tvoří okraj plátu.Implicitně se dá zapsat jako:
\begin{bmatrix} 1-u & -1 & u \end{bmatrix} \cdot C \cdot \begin{bmatrix} 1-v \\ -1 \\ v \end{bmatrix} = 0Povrch je pak tvořen body
C, které tuto rovnici splňují.Explicitně se dá zapsat jako:
P(u, v) = \begin{bmatrix} 1 - u & u \end{bmatrix} \cdot \begin{bmatrix} P_{0, v} \\ P_{1, v} \end{bmatrix} + \begin{bmatrix} P_{u, 0} & P_{u, 1} \end{bmatrix} \cdot \begin{bmatrix} 1 - v \\ v \end{bmatrix} - \begin{bmatrix} 1 - u & u \end{bmatrix} \cdot \begin{bmatrix} P_{0, 0} & P_{0, 1} \\ P_{1, 0} & P_{1, 1} \end{bmatrix} \cdot \begin{bmatrix} 1 - v \\ v \end{bmatrix}Zásadním nedostatek těchto ploch je, že není snadné vyjádřit tečné vektory na okrajích, a proto není snadné je napojovat na sebe.
-
Bikubické Coonsovy pláty
Podobné bilineárním, ale používájí Hermitovské polynomy:
\begin{aligned} F_1(t) &= 2t^3 - 3t^2 + 1 \\ F_2(t) &= -2t^3 + 3t^2 \\ \end{aligned}Implicitně je pak tento plát dán:
\begin{bmatrix} F_1(u) & -1 & F_2(u) \end{bmatrix} \cdot C \cdot \begin{bmatrix} F_1(v) \\ -1 \\ F_2(v) \end{bmatrix} = 0Stejně jako u bilineárních ploch, i tady je těžké získat tečné vektory na okrajích.
-
Obecná bikubická plocha
Kromě rohů je parametrizována i tečnými vektory na okrajích. Konečně tedy umožňuje snadné navazování.
Bézierovy plochy
Aproximační plochy dány (m + 1) \times (n + 1) řídícími body. Jsou:
- snadno diferencovatelné,
- jednoduše se modelují,
- lze z nich relativně snadno spočítat průnik s paprskem,
- speciální případ NURBS ploch.
P(u, v) = \sum_{i=0}^m \sum_{j=0}^n B_i^m(u) \cdot B_j^n(v) \cdot \vec{a}_{i,j}
Kde B_i^m(u) a B_j^n(v) jsou Bernsteinovy polynomy.
Při změně jendoho z bodů se změní celá plocha, proto se často více plátů spojuje dohromady. Pro spojitost G^0 se musí rovnat řídící body na okrajích. Pro G^0 musí tečné vektory na okrajích být lineárně závislé.
Zobrazují se rekurzivním dělením (patch splitting). Využívá se algoritmu de Casteljau.
B-spline plochy
Aproximační plochy analogické B-spline křivkám, ale se dvěma parametry.
-
Jsou lepší pro modelování než Hermitovské nebo Bézierovy plochy, protože se lépe navazují, jelikož B-splajny stupně
kgarantují spojitostC^{k-1}. -
Změnou jednoho řídícího bodu nezměníme celou plochu, ale jen část.
-
Celá plocha leží v konvexním obalu řídících bodů.
-
Průchodu řídícím bodem lze dosáhnout zvýšením jeho násobnosti (a tak snížením spojitosti).
-
Invariantní k lineárním transformacím.
-
NURBS plochy
Standard v průmyslovém modelování. Umožňují definovat velké množstí ploch: free-form surfaces, plochy založené na přímkách a kuželosečkách, atd. 11 Jsou invariantní k lineárním transformacím i k perspektivní projekci.
S(u,v) = \sum_{i=1}^k \sum_{j=1}^l R_{i,j}(u,v) \mathbf{P}_{i,j}kde
\mathbf{P}_{i,j}jsou řídící body aR_{i,j}(u,v)jsou NURBS bázové funkce:R_{i,j}(u,v) = \frac {N_{i,n}(u) N_{j,m}(v) w_{i,j}} {\sum_{p=1}^k \sum_{q=1}^l N_{p,n}(u) N_{q,m}(v) w_{p,q}}N_{i,n}(u)aN_{j,m}(v)jsou B-spline bázové funkce stupněnam.w_{i,j}jsou váhy.
Tip
NURBS plochy se využívají v modelovací technice sweeping (šablonování), kdy se množina bodů pohybuje (posunuje, rotuje, ...) prostorem za vniku tělesa. 12
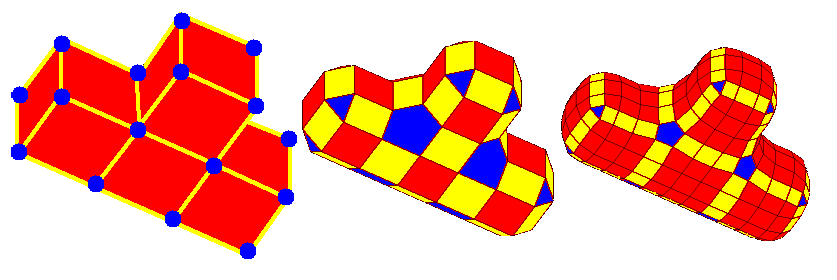
Surface subdivision / rekurzivní dělení polygonů
Polygonové povrchy dělíme v případě, kdy chceme je zjemnit, vyhladit.
-
Pravidla dělení
Dělení dodržují nějaké pravidlo.- Topologická pravidla: udávají vztahy pro generování nových vrcholů, hran, atd. z topologie objektu.
- Geometrická pravidla: generují nové vrcholy, hrany, atd. na základě intepolací sousedních vrcholů.
-
Extraordinary vertices / mimořádné vrcholy
Vrcholy, které mají jiný počet sousedů (valenci) než ostatní vrcholy.
-
4-point scheme
Interpolace
C^1křivkou. -
Catmull-Clark
Aproximuje původní mesh. Zachovává
C^2, na mimořádných bodech ale jenC^1. Po první iteraci vždy vznikou quady. Založený na bikubických uniformních B-splinech. -
Doo-Sabin
Aproximuje původní mesh. Narozdíl od Catmull-Clark je založený na bikvadratických uniformních B-splinech.
-
Loop
Aproximuje původní mesh. Funguje jen na trojúhelníkové síti.
-
Butterfly
Interpoluje původní mesh. Funguje jen na trojúhelníkové síti.
Další zdroje
-
Geometric Continuity of Parametric Curves: Three Equivalent Characterizations ↩︎
-
Sochor: PB009 Principles of Computer Graphics (jaro 2019) ↩︎