---
title: "Křivky a povrchy"
description: "TODO"
---
> [!NOTE]
> Implicitní a parametrické reprezentace. Interpolace a aproximace. Cn, Gn spojitost, podmínky spojitosti pro po částech definované funkce. Bézierovy křivky, B-spline křivky, ~NURBS,~ Coonsovy ~křivky a~ pláty. Povrchy tvořené rekurzivním dělením polygonů.
>
> _PB009, PA010_
## Druhy reprezentace
Jak povrchy tak křivky mohou být reprezentovány třemi způsoby:
### Explicitní reprezentace
Křivka nebo povrch je vyjádřen pomocí **funkce**.
```math
\begin{align*}
y &= f(x) & \text{ pro křivku} \\
z &= f(x, y) & \text{ pro povrch}
\end{align*}
```
Omezení na funkce je však příliš silné. Spoustu pěkných křivek a povrchů nelze vyjádřit pomocí jediné funkce.
### Implicitní reprezentace
Máme k dispozici rovnici ve tvaru:
```math
\begin{align*}
F(x, y) &= c & \text{ pro křivku} \\
F(x, y, z) &= c & \text{ pro povrch}
\end{align*}
```
kde $c$ je konstanta a je obvykle rovná 0.
Tato rovnice udává množinu bodů, ze které se křivka nebo povrch sestává. Takové množině se někdy říká _level set_ a metodám, které s nimi pracují _level-set methods_.
> [!IMPORTANT]
> Výhodou implicitně zadaných ploch je kompaktnější reprezentace a jednodušší ray casting. Nicméně výpočty s nimi jsou časově náročné, takže se stejně nejdřív převádí na polygonové meshe -- _polygonizace_.
> [!IMPORTANT]
> Tahle sekce přesahuje do [3D modelování a datové struktury](../szp04_3d_modelovani/) -> _Implicitní reprezentace a modelování_.
### Parametrická reprezentace
Udává **dráhu** pohybujícího se bodu, či něco jako **hladinu** povrchu. Snadno se z ní vyjadřuje tečna, čehož se využívá při jejich skládání.
Pro křivky:
```math
\begin{align*}
Q(t) &= \lbrack x(t), y(t), z(t) \rbrack & \text{ (bodová rovnice křivky)} \\
\vec{q}(t) &= (x(t), y(t), z(t)) & \text{ (vektorová rovnice křivky)}
\end{align*}
```
kde $t$ je "čas" z intervalu $\lbrack t_\text{min}, t_\text{max} \rbrack$, nejčastěji $\lbrack 0, 1 \rbrack$. Výhodné je, že takto zadaná křivka se může sama křížit, uzavírat, a podobně.
Analogicky pro povrchy:
```math
Q(u, v) = \lbrack x(u, v), y(u, v), z(u, v) \rbrack
```
kde pro $u$ a $v$ už metafora s časem nefunguje. Obvykle obě náleží do intervalu $\lbrack 0, 1 \rbrack$.
## Terminologie
Pro zbytek otázky je podstatné znát několik termínů:
- **Dotykový / tečný / tangent vektor křivky**\
Aktuální směr křivky v daném bodě. Z parametricky vyjádřené křivky $\vec{q}$ ho lze v čase $t_0$ získat jako derivaci:
```math
\vec{q}'(t_0) = \left(
\frac{\partial x(t_0)}{\partial t},
\frac{\partial y(t_0)}{\partial t},
\frac{\partial z(t_0)}{\partial t}
\right)
```
Rovnice tečny $\vec{p}$ je pak $\vec{p}(u) = \vec{q}(t_0) + \vec{q}'(t_0) \cdot u$.
- **Polynomiální křivka**\
Velmi častý druh křivek v počítačové grafice. Vypadají jako:
```math
Q_n(t) = a_0 + a_1 \cdot t + a_2 \cdot t^2 + \ldots + a_n \cdot t^n
```
Je velmi snadné je evaluovat a derivovat. Z nich často skládáme křivky po částech.
- **Kubika**\
Polynomiální křivka třetího stupně.
Parametricky:
```math
\begin{align*}
x(t) = a_{x}t^{3} + b_{x}t^{2} + c_{x}t + d_{x} \\
y(t) = a_{y}t^{3} + b_{y}t^{2} + c_{y}t + d_{y} \\
z(t) = a_{z}t^{3} + b_{z}t^{2} + c_{z}t + d_{z}
\end{align*}
```
Zapsáno pomocí matice:
```math
Q(t) = T \cdot C = \lbrack t^3, t^2, t, 1 \rbrack \cdot \begin{bmatrix}
a_x & a_y & a_z \\
b_x & b_y & b_z \\
c_x & c_y & c_z \\
d_x & d_y & d_z
\end{bmatrix}
```
Tečný vektor $\vec{q'}$ je pak:
```math
\vec{q'}(t) = \frac{\partial}{\partial t} \cdot C = \lbrack 3t^2, 2t, 1, 0 \rbrack \cdot C
```
U kubik platí, že $C = M \cdot G$, kde $M$ je bázová matice a $G$ je vektor geometrických podmínek.
- $T \cdot M$ definuje polynomiální bázi -- skupinu polynomů -- která je společná pro všechny křivky určitého typu.
- $G$ pak obsahuje parametry konkrétní křivky -- řídící a dotykové body.
- $t$ udává, jestli jsme na začátku či konci křivky.
- **Tečná rovina**\
Rovina, která se povrchu dotýká v konkrétním bodě a její normála je na povrch kolmá. Pro parametrickou plochu $Q$ je tečná plocha $T$ dána jako:
```math
\begin{align*}
\vec{q_{u}}(u,v) &= \frac{\partial Q(u,v)}{\partial u}
= \left(
\frac{\partial x(u,v)}{\partial u},
\frac{\partial y(u,v)}{\partial u},
{\partial z(u,v) \over \partial u}
\right) \\
\vec{q_{v}}(u,v) &= \frac{\partial Q(u,v)}{\partial v}
= \left(
\frac{\partial x(u,v)}{\partial v},
\frac{\partial y(u,v)}{\partial v},
{\partial z(u,v) \over \partial v}
\right) \\
T(r,s) &= Q(u,v) + r.\vec{q_{u}} + s.\vec{q_{v}}, \quad r,s \in \mathbb{R}
\end{align*}
```
kde $\vec{q_u}$ je tečný vektor ve směru parametru $u$, a analogicky $\vec{q_v}$
- **Normála / kolmice**\
Normálu $\vec{n}$ parametricky dané plochy $Q$ určíme jako vektorový součin tečných vektorů:
```math
\vec{n} = \frac{\vec{q_u} \times \vec{q_v}}{\left\lVert \vec{q_u} \times \vec{q_v} \right\rVert}
```
- **Gradient**\
Funkce, která vrací "směr a velikost největšího růstu". Nejčastěji se používá u povrchů k určení normály, ale lze ji použít v libovolné dimenzi k různým účelům. Pokud je povrch $f$ zadán implicitně, pak je gradient:
```math
\nabla f = \left(
\frac{\partial f}{\partial x},
\frac{\partial f}{\partial y},
\frac{\partial f}{\partial z}
\right)
```
## Interpolace a aproximace
- **Interpolace**\
Prokládání daných bodů křivkou. Konstrukce křivky, která interpolovanými body prochází.
V případě kubiky výše to znamená, že $G$ obsahuje body, kterými křivka prochází.
Mějmě funkci $f(x)$, jejíž hodnotu známe v bodech $f(x_0), f(x_1), \ldots, f(x_n)$. Interpolace znamená nalezení hodnot $f(x)$ pro všechna $x_0 < x < x_n$.
- **Aproximace**\
Přiblížení, odhad. Je nepřesným popisem nějaké jiné entity (např. čísla či funkce). Saháme k ní, pokud pro analytické řešení nemáme dost informací nebo výpočetní kapacity. Aproximace je méně přesná než interpolace, ale výpočetně jednodušší.
V případě kubiky výše to znamená, že $G$ obsahuje _řídící_ body, které sice udávají směr křivky, ale ta jimi neprochází.
## Spojitost
Představme si, že máme dva segmenty křivky: $Q_1$ a $Q_2$, spojené v bodě $t$, tedy $Q_1(t) = Q_2(t)$. Tento bod nazýváme _uzlem_ (knot). _Spojitost_ je zjednodušeně způsob, jakým jsou tyhle segmenty spojeny v uzlu.
### Parametrická spojitost stupně $n$ ($C^n$)
Křivka $Q$ patří do třídy $C^n$, pokud má ve všech bodech $t$ spojitou derivaci až do řádu $n$.
- $C^0$ -- dva segmenty jsou spojené; konečný bod jednoho segmentu je počátečním bodem druhého.
- $C^1$ -- platí $C^0$ a navíc je tečný vektor na konci prvního segmentu shodný s tečným vektorem na začátku druhého segmentu -- první derivace v uzlu jsou si rovny.
- $C^2$ -- platí $C^1$ a druhé derivace v uzlu jsou si rovny.
- $C^n$ -- platí $C^{n-1}$ a navíc jsou si $n$-té derivace v uzlu rovny.
- Bod pohybující se po $C^0$-spojité dráze sebou "trhne" **v prostoru**, když projde uzlem.
- V případě $C^1$ křivky se při průchodu uzlem směr ani rychlost prudce **nezmění**, může se však změnit zrychlení.
- V případě $C^2$ křivky se při průchodu uzlem **nezmění** už ani zrychlení.
### Geometrická spojitost stupně $n$ ($G^n$)
Je podobná parametrické spojitosti, ale vyžaduje jen "geometrickou" spojitost. Vyžaduje, aby si derivace byly **sobě úměrné**. [^mallinus] [^geometric-continuity]
- $G^0$ -- koncový bod prvního segmentu je totožný s počátečním bodem druhého segmentu ($C^0 = G^0$).
- $G^1$ -- platí $G^0$ a navíc je **směr** tečny na konci prvního segmentu shodný s **směrem** tečny na začátku druhého segmentu. **Velikost tečného vektoru (rychlost) se však může prudce změnit.**
- $G^2$ -- platí $G^1$ a navíc mají stejný **střed křivosti** (center of curvature). [^smoothness]
Platí, že $C^n \Rightarrow G^n$, ale obráceně $G^n \not\Rightarrow C^n$.
> [!NOTE]
> Podle slidů z PB009 musí faktor úměrnosti být různý od 0. [^pb009-2019] Podle Barskyho a DeRoseho musí v první derivaci být $> 0$ a v dalších už je to šumák. [^geometric-continuity] Co je správně? Kdo ví. Nemám dost častu to zjistit, takže to ponechávám jako cvičení čtenáři.
## Křivky
### Lagrangeův interpolační polynom
Základní metoda interpolace funkce, jejíž hodnotu známe jen v $n + 1$ diskrétních bodech $P_0, P_1, ... P_n$. Sestává se z pomocných polynomů $\ell_i$: [^lagrange]
```math
\ell_i(x) = \prod_{0 \le k \le n, k \neq i}^n \frac{x - x_k}{x_i - x_k}
```
Který splňuje podmínku:
```math
\ell_i(x_k) = \begin{cases}
1 & \text{ pro } i = k \\
0 & \text{ pro } i \neq k
\end{cases}
```
Pak polynom $P$ interpoluje danou množinu bodů:
```math
P(x) = \sum_{i=0}^n P_i \ell_i(x)
```
Blbé je, že musíme všechny pomocné polynomy přepočítat, když přidáme nový bod.
- **Hornerovo schéma / Horner's method**\
Metoda evaluace polynomů. Vychází z myšlenky, že násobení se dá nestovat: [^horner]
```math
\begin{aligned}
& a_0 + a_1 \cdot x + a_2 \cdot x^2 + ... + a_n \cdot x_n \\
& = a_0 + x(a_1 + x(a_2 + ... + x(a_{n-1} + x \cdot a_n)...))
\end{aligned}
```
Vyžaduje jen $n$ násobení a $n$ sčítání, což je optimální.
### Hermitovské křivky
Asi nejznámnější interpolační křivky v počítačové grafice. Jsou určeny dvěma řídícími body -- $P_0$ a $P_1$ -- a dvěma dotykovými vektory -- $\vec{p_0'}$ a $\vec{p_1'}$. Řídící body určují začátek a konec křivky, dotykové vektory její směr a vyklenutí. Pokud jsou oba vektory nulové, je to úsečka.
Je jednoduché je na sebe navázat v $C^1$, neboť tečné vektory jsou přímo součástí definice.
- **Cubic Hermite spline / Ferguson curve**\
Pro Hermitovskou kubiku platí: [^hermite-spline] [^ferguson]
```math
\begin{aligned}
Q(t) &=
\begin{bmatrix}
t^{3} & t^{2} & t & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
2 & -2 & 1 & 1 \\
-3 & 3 & -2 & -1 \\
0 & 0 & 1 & 0 \\
1 & 0 & 0 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
P_{0} \\
P_{1} \\
\vec{p'}_{0} \\
\vec{p'}_{1}
\end{bmatrix} = \\
&= P_0 \cdot F_1(t) + P_1 \cdot F_2(t) + \vec{p'}_0 \cdot F_3(t) + \vec{p'}_1 \cdot F_4(t)
\end{aligned}
```
kde $F_1, F_2, F_3, F_4$ jsou Hermitovské polynomy 3. stupně:
```math
\begin{aligned}
\textcolor{red}{F_1(t)} &= 2t^3 - 3t^2 + 1 \\
\textcolor{blue}{F_2(t)} &= -2t^3 + 3t^2 \\
\textcolor{green}{F_3(t)} &= t^3 - 2t^2 + t \\
\textcolor{cyan}{F_4(t)} &= t^3 - t^2
\end{aligned}
```
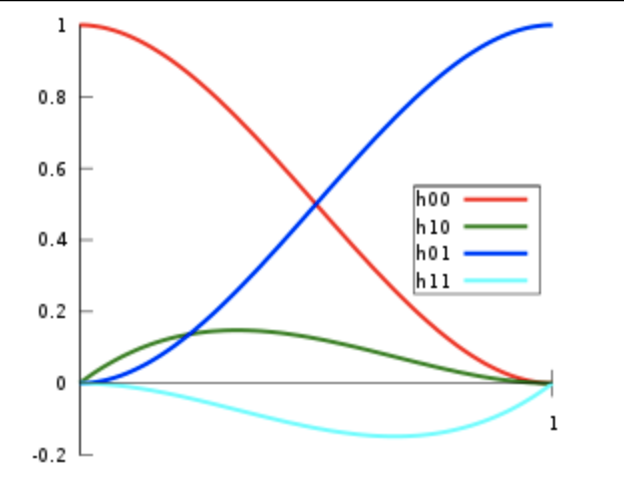
### Bézierova křivka
Asi nejčastěji používaná **aproximační** křivka. Využívá se zejména ve 2D grafice, třeba při definici fontů.
- Bézierova křivka $n$-tého stupně je definována $n + 1$ řídícími body $P_0, P_1, ... P_n$.
- Změnou polohy jednoho bodu dojde ke změně celé křivky. Proto se často dělí na segmenty menšího stupně, které se pak navazují na sebe.
Základem jsou **Bernsteinovy polynomy** $n$-tého stupně:
[stem]
b\_{\nu,n}(x) = \binom{n}{\nu} x^{\nu} \left( 1 - x \right)^{n - \nu}, \quad \nu = 0, \ldots, n,
Mezi jejich vlastnosti patří:
- Nezápornost: $b_{\nu,n}(x) \ge 0$ pro $x \in \lbrack 0, 1 \rbrack$.
- Jejich součet je roven jedné: $\sum_{\nu = 0}^n b_{\nu,n}(x) = 1$.
- Dají se vyjádřit rekurzí: $b_{\nu,n}(x) = (1 - x) \cdot b_{\nu,n-1}(x) + x \cdot b_{\nu-1,n-1}(x)$.
**Bernstein basis polynomials for 4th degree curve blending by [VisorZ](https://commons.wikimedia.org/w/index.php?curid=40129768)**

- **DeCasteljau algorithm**\
Rekurzivní algoritmus pro konstrukci Bézierových křivek. Využívá vlastností Bernsteinových polynomů.

- **Bézierova kubika**\
Bézierova křivka třetího stupně. Je dána čtyřmi řídícími body $P_0, P_1, P_2, P_3$:
```math
P(t) = (1 - t)^3 \cdot P_0 + 3 \cdot (1 - t)^2 \cdot t \cdot P_1 + 3 \cdot (1 - t) \cdot t^2 \cdot P_2 + t^3 \cdot P_3
```
### B-spline
- **Splajn / spline**\
Splajn stupně $n$ po částech definovaná polynomiální funkce stupně $n-1$ proměnné $x$. [^bspline]
_Po částech definovaná / piecewise_ znamená, že má několik intervalů a pro každý z nich jiný polynom.
- Místa, kde se části polynomu dotýkají jsou _uzly_ a jsou značeny pomocí $t_0, t_1, ..., t_n$ a řazeny v neklesajícím pořadí.
- Pokud jsou uzly unikátní, pak je splajn v uzlech $C^{n-2}$ spojitý. [^bspline]
- Pokud je $r$ uzlů shodných, je v tomto místě pouze $C^{n-r-1}$ spojitý.
---
**Basis spline / B-spline** stupně $n$ je aproximační křivka / splajn daná sekvencí $n$ uzlů. Jako funkce vrací užitečné hodnoty jen mezi prvním a posledním uzlem, všude jinde je nulová. Svůj název dostala podle toho, že B-splajny slouží jako bázové funkce pro splajnové křivky.
Lze ji definovat pomocí **Cox-de Boorovy** rekurzivní formule:
> [!TIP]
> de Boorův algoritmus je generalizací DeCasteljauova algoritmu ale pro B-splajny.
```math
\begin{aligned}
B_{i,0}(x) &= \begin{cases}
1 & \text{pro } t_i \le x < t_{i+1} \\
0 & \text{jinak}
\end{cases}
\\
B_{i,n}(x) &= \textcolor{red}{\frac{x - t_i}{t_{i+n} - t_i}} B_{i,n-1}(x)
+ \textcolor{blue}{\frac{t_{i+n+1} - x}{t_{i+n+1} - t_{i+1}}} B_{i+1,n-1}(x)
\end{aligned}
```
Zatímco $x$ jde od $t_i$ k $t_{i+n}$, červený výraz začíná na 1 a klesá k 0.
Podobně, zatímco $x$ jde od $t_{i+1}$ k $t_{i+n+1}$, modrý výraz začíná na 0 a roste k 1.
Navíc platí $\sum_{i=0}^{n} B_{i,n}(x) = 1$.
Jejich užitečnost spočívá v tom, že libovolný splajn stupně $n$ daný sekvencí uzlů lze vyjádřit jako lineární kombinaci B-splajnů:
```math
S(x) = \sum_{i=0} c_i B_{i,n}(x)
```
> [!NOTE]
> Uzlů je zpravidla víc než $n+1$, protože pak teprve máme víc než jeden B-spline, který kombinujeme.
- **Uniformní B-splajny**\
Uzly jsou rozloženy rovnoměrně. Tedy mezi každými dvěma uzly $t_i$ a $t_{i+1}$ je stejná vzdálenost $h$.
Příklad:
```math
T = \begin{bmatrix}
t_0 & t_1 & t_2 & t_3
\end{bmatrix}
= \begin{bmatrix}
0 & 0.\overline{3} & 0.\overline{6} & 1
\end{bmatrix}
```
- **Coonsova kubika**\
Kubika $P$ daná 4 řídícími body $P_0, P_1, P_2, P_3$. Neprochází ani jedním z kontrolních bodů. [^coons]
```math
\begin{aligned}
P(t) &= B_0(t) \cdot P_0 + B_1(t) \cdot P_1 + B_2(t) \cdot P_2 + B_3(t) \cdot P_3, t \in \lbrack 0, 1 \rbrack \\
B_0(t) &= \frac{1}{6} (1 - t)^3 \\
B_1(t) &= \frac{1}{6} (3t^3 - 6t^2 + 4) \\
B_2(t) &= \frac{1}{6} (-3t^3 + 3t^2 + 3t + 1) \\
B_3(t) &= \frac{1}{6} t^3
\end{aligned}
```
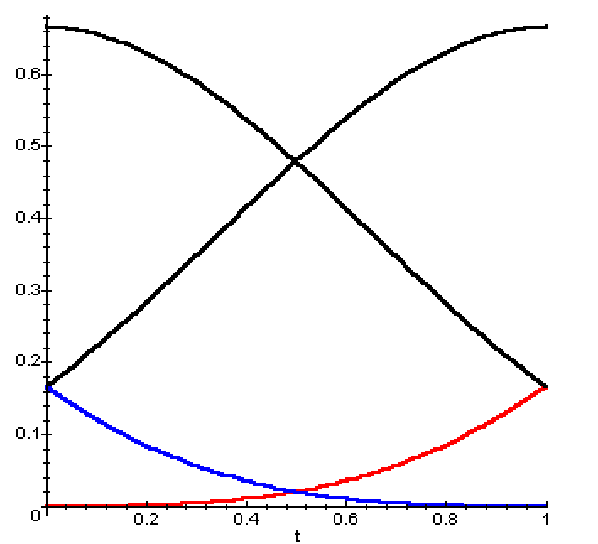
> [!NOTE]
> Něco ohledně tohohle termínu mi hrozně smrdí. Zdá se, že jediní, kdo používají "coons cubic curve" jsme my a ČVUT.
## Povrchy
Interpolace je náročná, proto se častěji používají aproximační povrchy.
### Interpolační plocha
Plocha $\vec{P}$.
Dáno:
- $(m + 1) \times (n + 1)$ řídících bodů $\vec{P}_{i,j}$.
- $m + 1$ hodnot $u_k$ a $n + 1$ hodnot $v_l$.
Platí, že $\vec{P}(u_k, u_l) = \vec{P}_{k,l}$ pro $k = 0, 1, ..., m$ a $l = 0, 1, ..., n$.
Interpolujeme vektorovým polynomem $\vec{a}_{i,j}$:
```math
\vec{P}(u, v) = \sum_{i = 0}^m \sum{j = 0}^n \vec{a}_{i,j} \cdot u^i \cdot v^j
```
V případě Lagrangeova polynomu je $\vec{a}_{i,j} = \ell_i^m(u) \cdot \ell_j^n(v)$.
### Hermitovský plát
Interpolační povrch.
- **12-ti vektorová varianta**\
4 rohové body a 8 tečných vektorů.
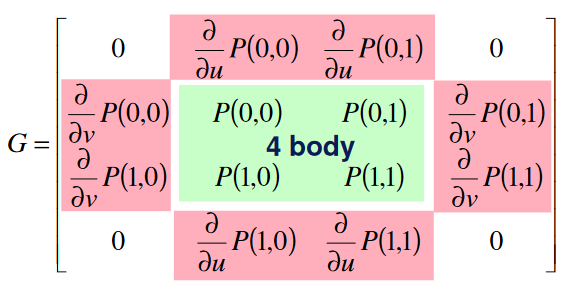
- **16-ti vektorová varianta**\
4 rohové body, 8 tečných vektorů a 4 zkrutové vektory.
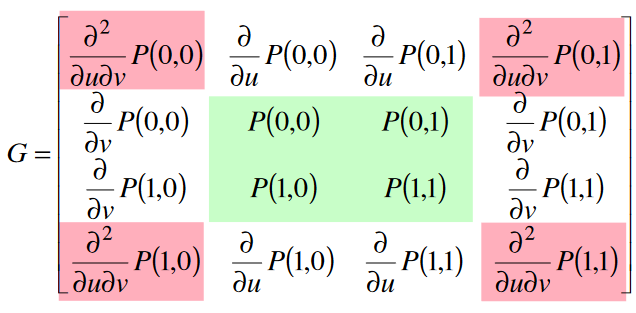
### Coonsovy pláty / Coonsovy plochy / Coons patch
Plochy vzniknuvší interpolací mezi křivkami udávající jejich okraje. Dají se na sebe pěkně napojovat, právě protože jsou definovány svými okraji.
> [!WARNING]
> Coonsovy pláty jsou **interpolační**, zatímco Coonsovy křivky jsou **aproximační**.
- **Bilineární Coonsovy pláty**
Určeny 4 křivkami $P(u, 0), P(u, 1), P(0, v), P(1, v)$, které tvoří okraj plátu.
Implicitně se dá zapsat jako:
```math
\begin{bmatrix}
1-u & -1 & u
\end{bmatrix}
\cdot
C
\cdot
\begin{bmatrix}
1-v \\ -1 \\ v
\end{bmatrix}
= 0
```
Povrch je pak tvořen body $C$, které tuto rovnici splňují.
Explicitně se dá zapsat jako:
```math
P(u, v) = \begin{bmatrix} 1 - u & u \end{bmatrix} \cdot \begin{bmatrix} P_{0, v} \\ P_{1, v} \end{bmatrix}
+ \begin{bmatrix} P_{u, 0} & P_{u, 1} \end{bmatrix} \cdot \begin{bmatrix} 1 - v \\ v \end{bmatrix}
- \begin{bmatrix} 1 - u & u \end{bmatrix} \cdot
\begin{bmatrix}
P_{0, 0} & P_{0, 1} \\
P_{1, 0} & P_{1, 1}
\end{bmatrix}
\cdot \begin{bmatrix} 1 - v \\ v \end{bmatrix}
```
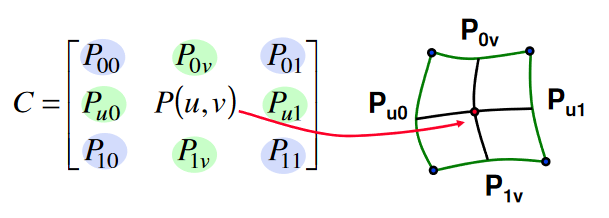
Zásadním nedostatek těchto ploch je, že není snadné vyjádřit tečné vektory na okrajích, a proto není snadné je napojovat na sebe.
- **Bikubické Coonsovy pláty**
Podobné bilineárním, ale používájí Hermitovské polynomy:
```math
\begin{aligned}
F_1(t) &= 2t^3 - 3t^2 + 1 \\
F_2(t) &= -2t^3 + 3t^2 \\
\end{aligned}
```
Implicitně je pak tento plát dán:
```math
\begin{bmatrix}
F_1(u) & -1 & F_2(u)
\end{bmatrix}
\cdot
C
\cdot
\begin{bmatrix}
F_1(v) \\ -1 \\ F_2(v)
\end{bmatrix}
= 0
```
Stejně jako u bilineárních ploch, i tady je těžké získat tečné vektory na okrajích.
- **Obecná bikubická plocha**
Kromě rohů je parametrizována i tečnými vektory na okrajích. Konečně tedy umožňuje snadné navazování.
### Bézierovy plochy
Aproximační plochy dány $(m + 1) \times (n + 1)$ řídícími body. Jsou:
- snadno diferencovatelné,
- jednoduše se modelují,
- lze z nich relativně snadno spočítat průnik s paprskem,
- speciální případ NURBS ploch.
```math
P(u, v) = \sum_{i=0}^m \sum_{j=0}^n B_i^m(u) \cdot B_j^n(v) \cdot \vec{a}_{i,j}
```
Kde $B_i^m(u)$ a $B_j^n(v)$ jsou Bernsteinovy polynomy.

Při změně jendoho z bodů se změní celá plocha, proto se často více plátů spojuje dohromady. Pro spojitost $G^0$ se musí rovnat řídící body na okrajích. Pro $G^0$ musí tečné vektory na okrajích být lineárně závislé.
Zobrazují se rekurzivním dělením (patch splitting). Využívá se algoritmu de Casteljau.
### B-spline plochy
Aproximační plochy analogické B-spline křivkám, ale se dvěma parametry.
- Jsou lepší pro modelování než Hermitovské nebo Bézierovy plochy, protože se lépe navazují, jelikož B-splajny stupně $k$ garantují spojitost $C^{k-1}$.
- Změnou jednoho řídícího bodu nezměníme celou plochu, ale jen část.
- Celá plocha leží v konvexním obalu řídících bodů.
- Průchodu řídícím bodem lze dosáhnout zvýšením jeho násobnosti (a tak snížením spojitosti).
- Invariantní k lineárním transformacím.
- **NURBS plochy**
Standard v průmyslovém modelování. Umožňují definovat velké množstí ploch: free-form surfaces, plochy založené na přímkách a kuželosečkách, atd. [^nurbs] Jsou invariantní k lineárním transformacím i k perspektivní projekci.
```math
S(u,v) = \sum_{i=1}^k \sum_{j=1}^l R_{i,j}(u,v) \mathbf{P}_{i,j}
```
kde $\mathbf{P}_{i,j}$ jsou řídící body a $R_{i,j}(u,v)$ jsou NURBS bázové funkce:
```math
R_{i,j}(u,v) = \frac {N_{i,n}(u) N_{j,m}(v) w_{i,j}} {\sum_{p=1}^k \sum_{q=1}^l N_{p,n}(u) N_{q,m}(v) w_{p,q}}
```
$N_{i,n}(u)$ a $N_{j,m}(v)$ jsou B-spline bázové funkce stupně $n$ a $m$. $w_{i,j}$ jsou váhy.
> [!TIP]
> NURBS plochy se využívají v modelovací technice _sweeping_ (šablonování), kdy se množina bodů pohybuje (posunuje, rotuje, ...) prostorem za vniku tělesa. [^sweeping]
## Surface subdivision / rekurzivní dělení polygonů
Polygonové povrchy dělíme v případě, kdy chceme je zjemnit, vyhladit.
- **Pravidla dělení**\
Dělení dodržují nějaké pravidlo.
- _Topologická pravidla_: udávají vztahy pro generování nových vrcholů, hran, atd. z topologie objektu.
- _Geometrická pravidla_: generují nové vrcholy, hrany, atd. na základě intepolací sousedních vrcholů.
- **Extraordinary vertices / mimořádné vrcholy**
Vrcholy, které mají jiný počet sousedů (valenci) než ostatní vrcholy.
- **4-point scheme**
Interpolace $C^1$ křivkou.
- **Catmull-Clark**
Aproximuje původní mesh. Zachovává $C^2$, na mimořádných bodech ale jen $C^1$. Po první iteraci vždy vznikou quady. Založený na bikubických uniformních B-splinech.
- **Doo-Sabin**
Aproximuje původní mesh. Narozdíl od Catmull-Clark je založený na **bikvadratických** uniformních B-splinech.
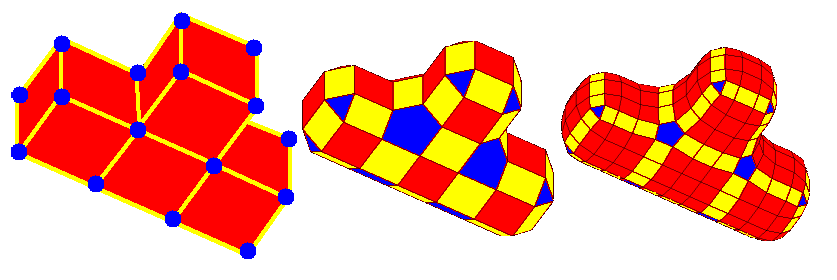
- **Loop**
Aproximuje původní mesh. Funguje jen na trojúhelníkové síti.
- **Butterfly**
**Interpoluje** původní mesh. Funguje jen na trojúhelníkové síti.
[^pa010-2021]: Byška, Furmanová, Kozlíková, Trtík: PA010 Intermediate Computer Graphics (podzim 2021)
[^pa010-2020]: Sochor: PA010 Intermediate Computer Graphics (podzim 2020)
[^pb009-2019]: Sochor: PB009 Principles of Computer Graphics (jaro 2019)
[^smoothness]: [Wikipedia: Smoothness](https://en.wikipedia.org/wiki/Smoothness)
[^mallinus]: [Jaakko Kurhila and Matti Mäkelä: Parametric Curves](https://www.cs.helsinki.fi/group/goa/mallinnus/curves/curves.html)
[^geometric-continuity]: [Geometric Continuity of Parametric Curves: Three Equivalent Characterizations](https://ieeexplore.ieee.org/document/41470)
[^lagrange]: [Wikipedia: Lagrange polynomial](https://en.wikipedia.org/wiki/Lagrange_polynomial)
[^bspline]: [Wikipedia: B-spline](https://en.wikipedia.org/wiki/B-spline)
[^hermite-spline]: [Wikipedia: Cubic Hermite spline](https://en.wikipedia.org/wiki/Cubic_Hermite_spline)
[^ferguson]: [ČVUT: Ferguson curve](https://marian.fsik.cvut.cz/~kongo/download/pcgr/lectures/01%20crv_ferg.pdf)
[^coons]: [ČVUT: Coons curve](https://marian.fsik.cvut.cz/~kongo/download/pcgr/lectures/03%20crv_coons.pdf)
[^coons-path]: [Wikipedia: Coons patch](https://en.wikipedia.org/wiki/Coons_patch)
[^nurbs]: [Wikipedia: Non-uniform rational B-spline](https://en.wikipedia.org/wiki/Non-uniform_rational_B-spline)
[^sweeping]: [Wikipedia: Solid modeling](https://en.wikipedia.org/wiki/Solid_modeling#Sweeping)
[^horner]: [Wikipedia: Horner's method](https://en.wikipedia.org/wiki/Horner%27s_method)
## Další zdroje
- [NURBS Calculator](http://nurbscalculator.in/)
- [ČVUT: Computer Graphics](https://mat.fs.cvut.cz/computer-graphics/)