fi-notes/SZP04_3d_modelovani.md at 8f522568d5c2009e876d7513fe22cfee422f31dc

Vojtěch Struhár 8f522568d5 Regex fix lt symbols

Just global search and replace in vs code

2025-06-07 00:58:21 +02:00

18 KiB

Raw Blame History

title	description
3D modelování a datové struktury	TODO

Note

Mnohoúhelníkové a trojúhelníkové sítě: datové struktury, modelování, pass:[<s>filtrování</s>], změna struktury sítě, *zjednodušování sítě**. Implicitní a parametrické* reprezentace a modelování (SDF, CSG, B-Rep).
PA010

Mnohoúhelníkové a trojúhelníkové sítě

Základní pojmy

Geometrie
- Mění jí deformace.
- Např. to, kde jsou body.
- Zahrnuje zakřivení (curvature), plochu (area), vzdálenosti mezi body, atd. pa010-2021
Topologie
- Nemění ji deformace.
- Např. to jak jsou body propojené.
- Sousednost (neighborhood), souvislost (connectedness), adjacency. atd. pa010-2021
  
  Topology topology
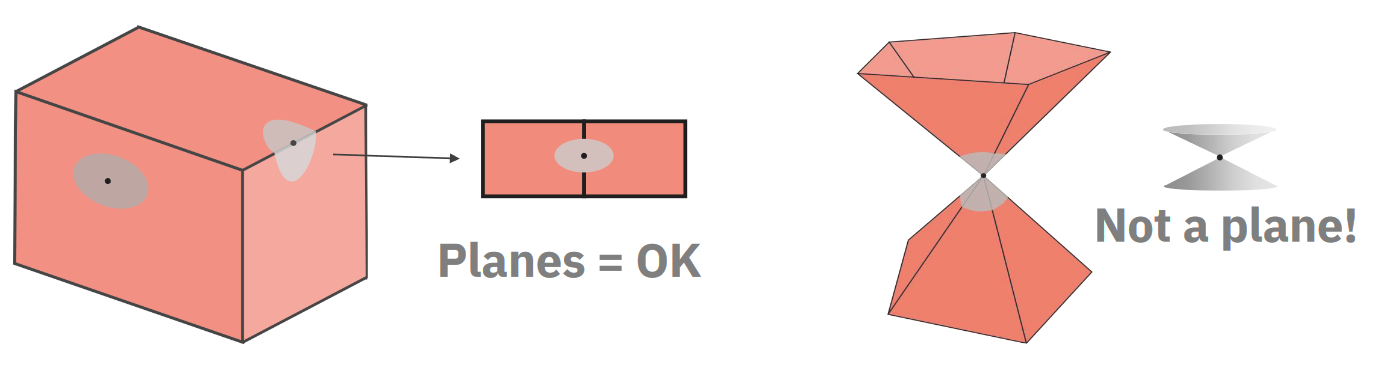
Topological manifold
Prostor/útvar, který lokálně připomíná (je homeomorfní) $n$-dimenzionální Euklidovský prostor. pa010-2021 manifold-wiki

$n$-manifold je takový topologický manifold, kde okolí každého bodu je homeomorfní s $n$-dimenzionálním Euklidovským prostorem. manifold-wiki

Manifoldy jsou typicky fyzikálně validní a efektivní (např. pomocí half-edge).
- Souřadnicový prostor \mathbb{R}^n je $n$-manifold.
- Libovolný diskrétní prostor je 0-manifold.
- Kruh je 1-manifold.
- Torus (donut) a Kleinova láhev je 2-manifold (povrch).
- Každý povrch je 2-manifold až na neuzavřené hrany. pa010-2021
- $n$-dimenzionální koule je $n$-manifold.
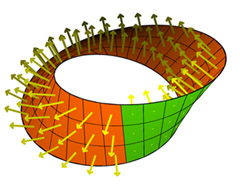
Orientability / orientace
- Orientable surfaces allow consistent definition of clockwise and counter-clockwise orientation.
  - We can define front/back or inner/outer side.
- In non-orientable surfaces, the orientation can change after running through a surface loop.
— PA010
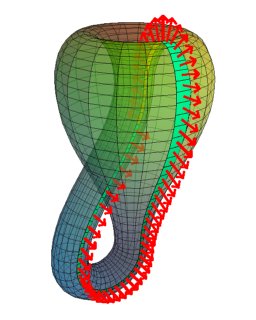
Möbiova páska a Kleinova láhev

Möbiova páska je neorientovatelná, protože po oběhnutí pásu se změní orientace.

Kleinova láhev je orientovatelná, protože po oběhnutí láhve se orientace nezmění.
Elementy topologie
- Vertices (vertexy / vrcholy) (V)
- Edges (hrany) (E)
- Faces (stěny) (F)
- Genus (G)
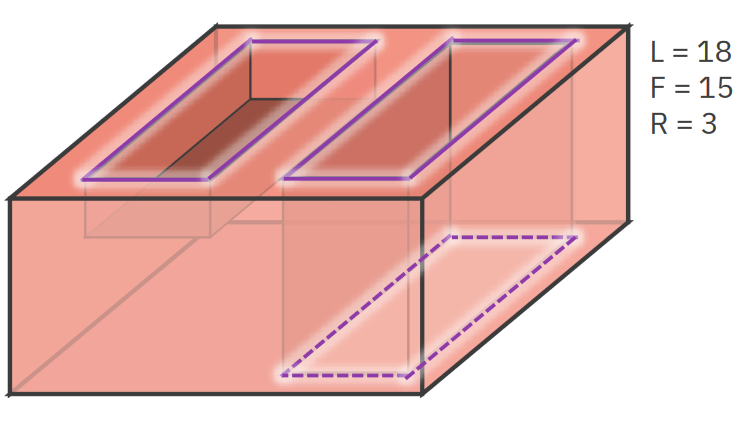
- Edge loops (L)
- Boundary edge loops (rings, R)
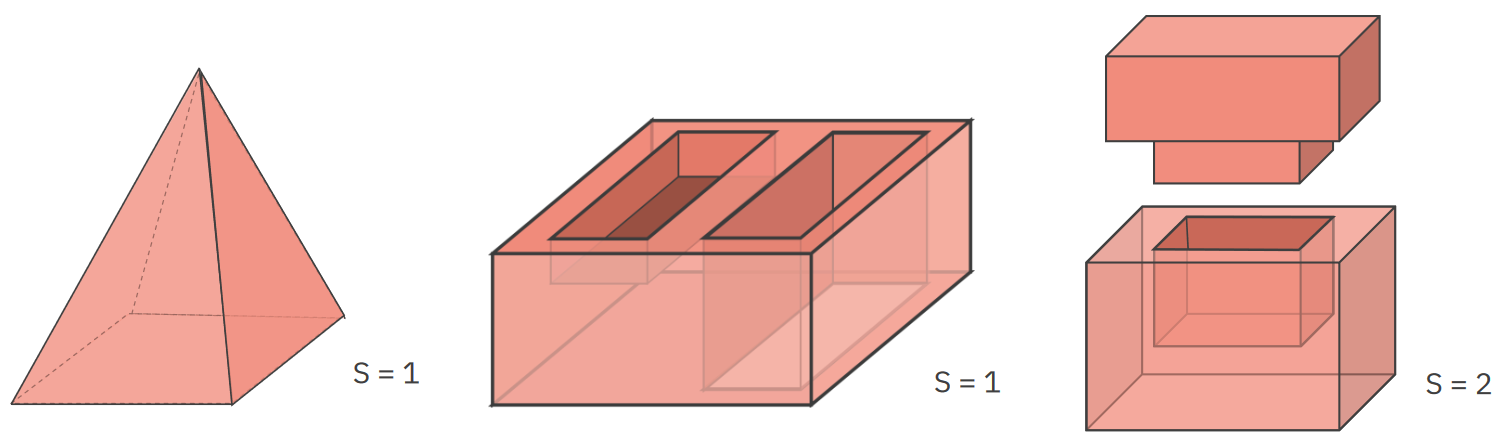
- Shells (S)
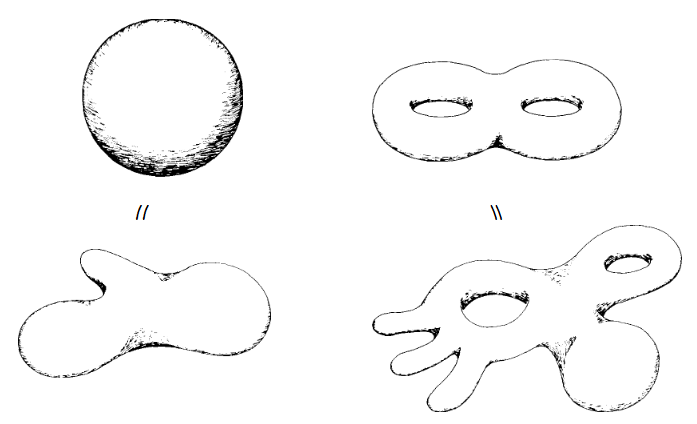
Genus
- Počet "děr" v povrchu.
- Počet "držadel" v povrchu.
- Počet skupin křivek, které nelze stáhnout do bodu.
  
  Genus of an orientable surface is the maximum number of cuttings along nonintersecting simple closed curves without separating it.
  
  — PA010
  
  Tip
  
  Podle Wikipedie je genus česky rod plochy.
  
  Tip
  
  Je to maximální počet těch řezů.
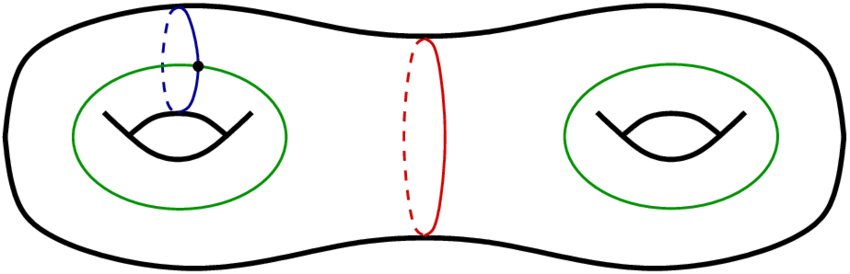
  Následující povrchgenus jde rozdělit podél červené křivky na dva, ale neuvažujeme ji, protože chceme nejvyší možný počet řezů, které povrch nerozdělí.
Boundary edge loops / rings
Edge loops uvnitř stěn, které nejsou vnějšími hranicemi objektu.

"Díry" ve stěnách, ale není to genus.

R = L - F
Shells (S)
Spojené komponenty povrchu (množiny stěn).
Eulerova charakteristika / Euler-Poincaré formula
Eulerova charakteristika \chi popisuje topologický prostor či geometrický útvar M. Je to topologický invariant -- nezmění se jakkoli je tento útvar pozohýbán.
```
\chi(M) = V - E + F \text{ (bez děr)} \\
\chi(M) = V - E + F - R = 2 \cdot (S - G) \text{ (s děrami)}
```
Important

Pro libovolný mnohostěn (polyhedron) bez děr je \chi = 2.
Important

Pro uzavřený 2-manifoldní trojúhelníkový mesh:
Každý trojúhelník má 3 hrany a každá hrana je sdílena dvěma trojúhelníky, takže E = \frac{3}{2} F.
💡 TIP\

Intuitivně: pokud jsme neúsporní, pak máme tři hrany pro každý trojúhelník (3F), každou hranu ale "přilepíme" k nějakému dalšímu trojúhelníku, takže každou hranu máme zbytečně dvakrát (2E), proto 3F = 2E, tedy E = \frac{3}{2} F.
Z Euler-Poincaré plyne, že
```
V = 2 + E - F = 2 + \frac{3}{2} F - F = 2 + \frac{1}{2} F \sim \frac{1}{2}
```
- Tedy platí poměr $E:F:V = 3:2:1$. - Tedy průmeřný vertex degree (počet hran, které vycházejí z vertexu) je $2 \cdot \frac{E}{V} \sim 6$.
Každá hrana (ve 2-manifoldu) přispívá k degree právě dvou vertexů, protože někde začíná a končí.
Kdybychom sečetli degree všech vertexů, dostali bychom $2E$, proto $2E \sim 6V$.
Simplex
Nejjednodušší polytop (generalizace mnohoúhelníku, mnohostěnu, atd.). Generalizace trojúhelníku v libovolné dimenzi:
- 0D -- bod
- 1D -- úsečka
- 2D -- trojúhelník
- 3D -- tetraedr
- 4D -- 5-cell (5nadstěn)

Datové struktury

Seznam trojúhelníků / list of triangles (polygon soup)
Jednoduchý, ale obsahuje redundantní informace. Neříká nic o sousednosti.
Indexed face set
Vrcholy trojúhelníků jsou dány pomocí indexů do pole vertexů. Méně redundantní, ale neříká nic o sousednosti.
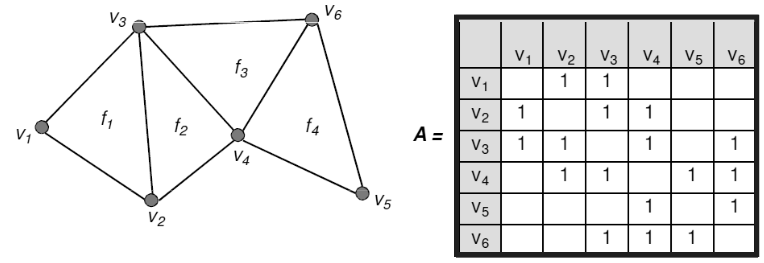
Adjacency matrix
Matice vertexů říkající, zda-li je mezi vertexy hrana. Nijak nereprezentuje faces.
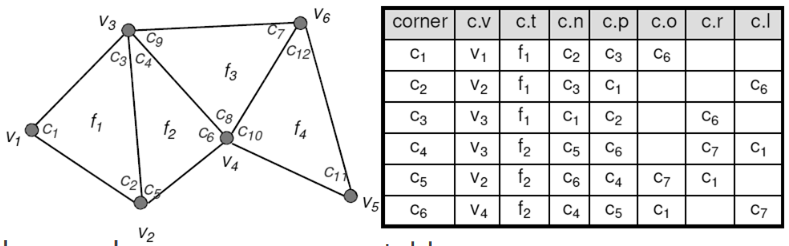
Corner table / tabulka rohů
Pro každý vertex udává sousední rohy. Fajn, pokud nás zajímá sousednost vertexů. Trochu redundantní. Použitelná jen pro trojúhelníkové sítě.
- c.v -- vertex rohu,
- c.t -- trojúhelník rohu,
- c.n -- následující roh trojúhelníku,
- c.p -- předchozí roh trojúhelníku,
- c.o -- opačný roh v sousedním trojúhelníku (opačný roh kdyby to byl quad).
- c.r -- "pravý" roh v sousedním trojúhelníku,
- c.l -- "levý" roh v sousedním trojúhelníku.

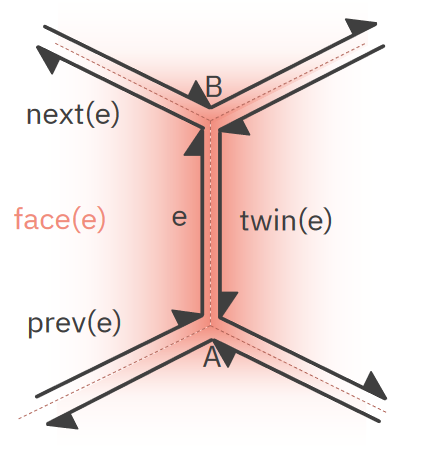
Half-edge data structure
Použitelná pro 2-manifoldy. Poskytuje rychlé hledání sousednosti. Umožňuje efektivní modifikace meshů.

record HalfEdge // e.g. e
{
    Vertex Start { get; set; } // e.g. A
    // NB: End is optional since you can easily access Twin.Start.
    Vertex End { get; set; } // e.g. B
    HalfEdge Twin { get; set; }

    HalfEdge Next { get; set; }
    // NB: Prev is optional since you can easily access Next.Next.
    HalfEdge Prev { get; set; }
    Face Face { get; set; }
}

Modelování

Important

Tahle sekce má docela průnik s otázkou Modelování 3D postav.

Boundary representation model (B-rep)
Modelování objektů pomocí jejich hranic -- boundaries (hrany, stěny, atd.).
Polygonální síť / mesh
Síť trojúhelníků. Hrany jsou vždy rovné. Potřebuje velké množství polygonů na hladké povrchy.
B-spline plochy
Vertexy řídící sítě slouží k aproximaci křivek. Nedokáže popsat libovolnou topologii.
Topologická validita
- B-rep model splňuje Euler-Poincaré formuli. (Což neimplikuje, že je 2-manifold.)
- Sousedící faces mají stejnou orientaci.
- Žádné faces "nevisí" ven z modelu.
Geometrická validita
Numerické chyby v geometrii (např. v pozicích vertexů) mohou způsobit konflikty mezi topologickou a geometrickou informací. pa010-2021

Např.: Rovnice rovin tvrdí, že hrana je uvnitř objektu, ale topologie říká, že je mimo něj.
Eulerovy operátory
Operátory zachovávající Euler-Poincaré formuli. Jsou dostatečné pro konstrukci užitečných meshů. Pracují s 6 parametry: V -- vertices, E -- edges, F -- faces, H -- components, S -- shells, G -- genus. pa010-2021 boundaries

Note

Zdá se, že H -- components je ekvivalentní R -- rings.

Ač Eulerových operátorů se dá zadefinovat mnoho, v praxi stačí:

|==== | Operátor | Popis

| MSFV | make shell, face, vertex

| MEV | make edge, vertex

| MFE | make face, edge

| MSH | make shell, hole

| MEKL | make edge, kill loop

2+|

| KEV | kill edge, vertex

| KFE | kill face, edge

| KSFV | kill shell, face, vertex

| KSH | kill shell, hole

| KEML | kill edge, make loop |====

Regularizované booleovské operátory / regularized boolean operators
Reprezentace těles pomocí booleovských operací. Regularizované značí, že výsledek je vždy platné 2-manifold těleso.
- AND - průnik \cap^*
- OR - sjednocení \cup^*
- SUB - rozdíl \setminus^*
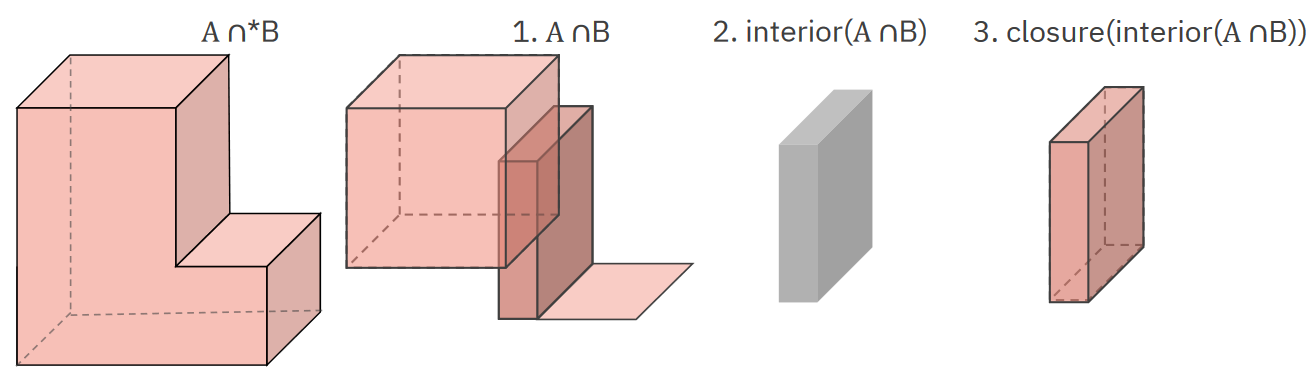
Regularizace vypadá tak, že nejprve je provedena booleovská operace, poté je vypočítán interior a následně closure. rbo
- Interior point p tělesa S je takový bod, že existuje r takové, že otevřená koule s poloměrem r a středem v p obsahuje jen body z S.
- Exterior point p tělesa S je takový bod, že existuje r takové, že otevřená koule s poloměrem r a střem v p nemá žádný průnik s S.
- Interior tělesa S je množina všech jeho interior pointů.
- Exterior tělesa S je množina všech jeho exterior pointů.
- Boundary tělesa S je množina bodů, které nejsou ani interior ani exterior tělesa S.
- Clusure tělesa S je sjednocení jeho interior a boundary.
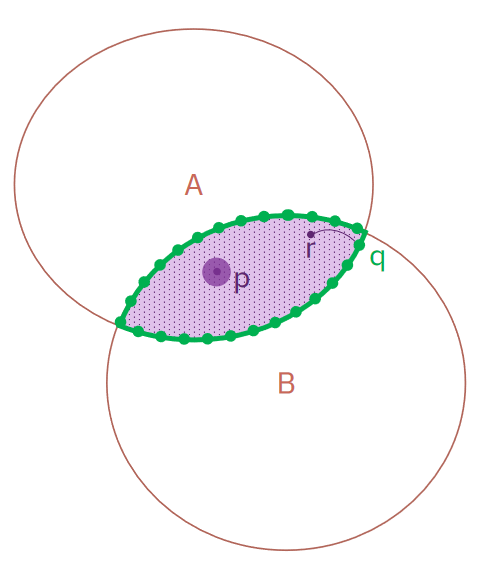
Otevřená koule je koule bez povrchu. Tedy právě ty body, které jsou jejím "vnitřkem".

Schéma interior and a boundary tělesa A \cap B pa010-2021

Příklad regularizovaného průniku pa010-2021
Global deformations (Alan Barr)
Mění tvar celého meshe. Obvykle jednoduché a snadno implementovatelné. Jsou fajn při modelování.
- Translace,
- Rotace,
- Škálování / scale,
- Zkosení / shear,
- Tapering / zúžení -- nekonstantní škálování,
  
  Tapering in 3ds Max
- Twisting / screw / šroubování -- nekonstantní rotace okolo osy,
  
  Twisting in 3ds Max
- Bending / ohýbání -- ohnutí rozsahu vertexů okolo daného bodu o daný úhel.
  
  Bending in Blender
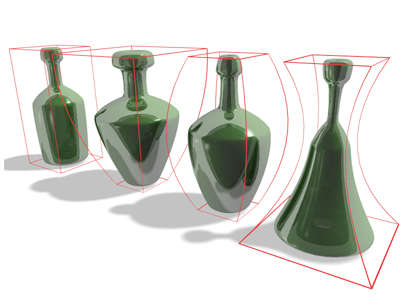
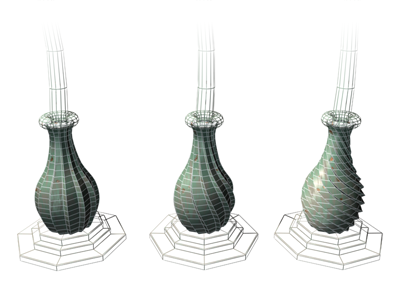
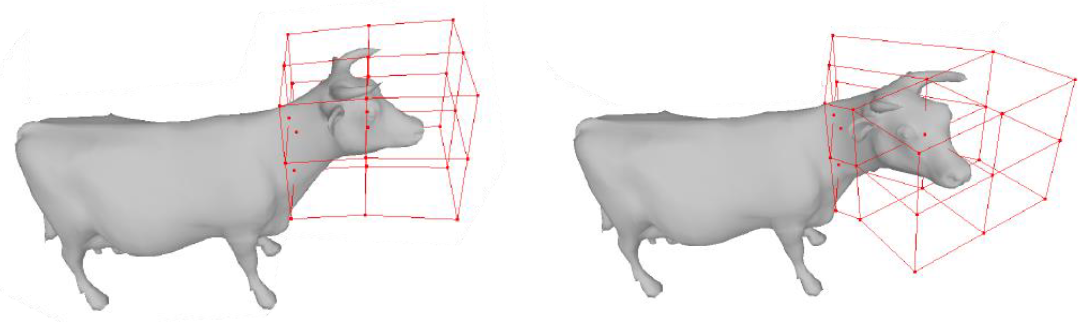
Free-form deformations (FFD)
Lokální deformace vertexů v dané "kleci" / mřížce / lattice -- Bezierově objemu.
1. Vyrob FFD mřížku (Bezierův objem).
2. "Umísti" do objemu objekt, který chceš deformovat.
3. Deformuj mřížku (hýbej s jejími body).
4. Transformuj vertexy v mřížce podle změn v FFD prostoru.
Má řadu rozšíření s různými tvary mřížky.

Změna struktury sítě

Important

Modifikace meshů mají značný přesah do otázky Křivky a povrchy a taky Pokročilá počítačová grafika

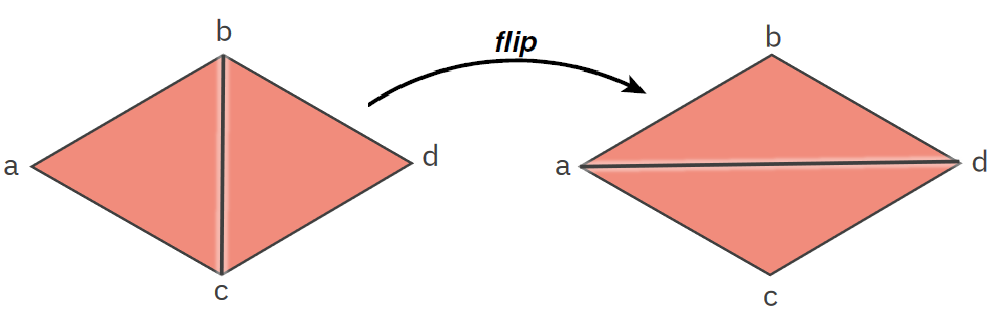
Překlápění hrany / edge flip
Lokální změna, která nahradí hranu (b,c) hranou (a,d). Trojúhelníky (a,b,c) a (b,d,c) se stanou (a,d,c) a (a,b,d). pa010-2021
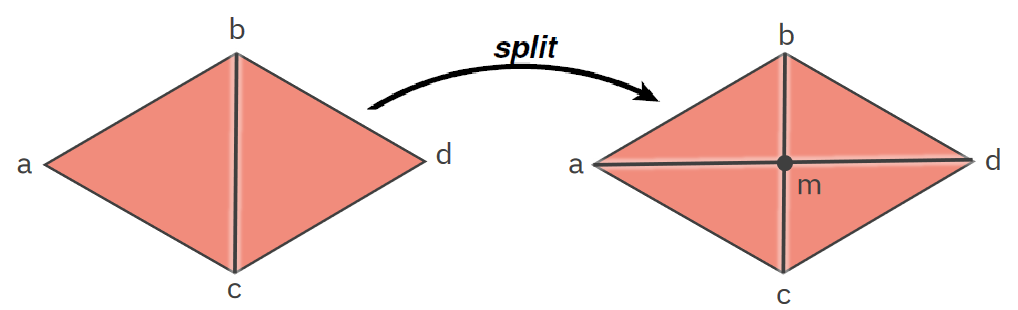
Rozdělení hrany / edge split
Lokální změna přidávající další vertex a hrany mezi dva trojúhelníky, které tak rozdělí na čtyři. pa010-2021
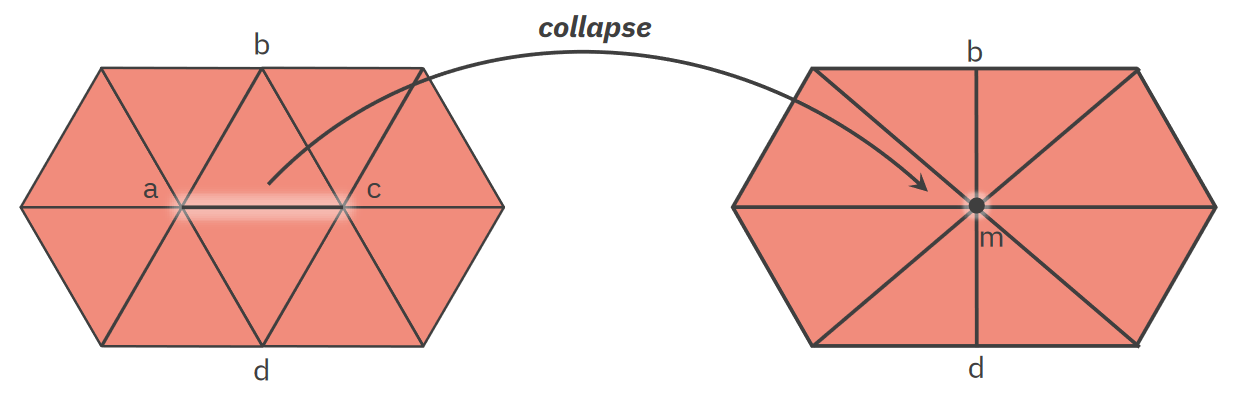
Zhroucení grany / edge collapse
Lokální změna, která nahrazuje hranu vrcholem. pa010-2021
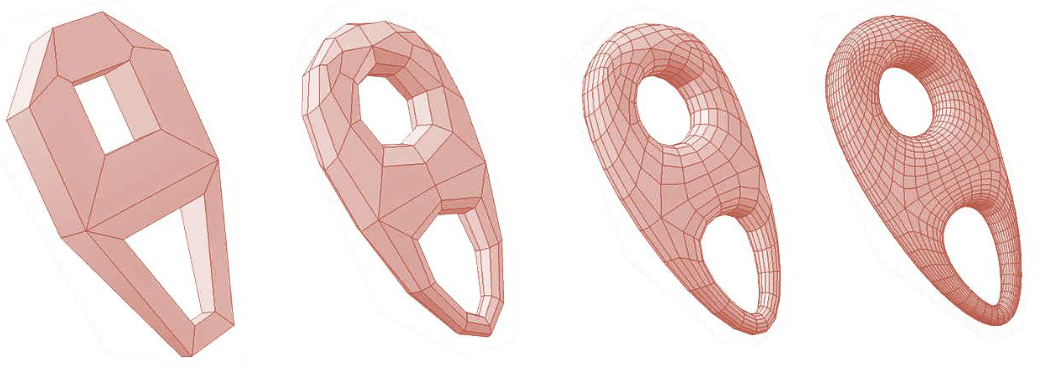
Upsampling / subdivision
Globální změna, která rozdělí jedno primitivum (trojúhelník / quad) na více. Vyhlazuje mesh dělením na menší kousky. pa010-2021
Downsampling / decimation / simplification
Globální redukce množství primitiv. Často využívá edge collapse.
Regularization / mesh resampling
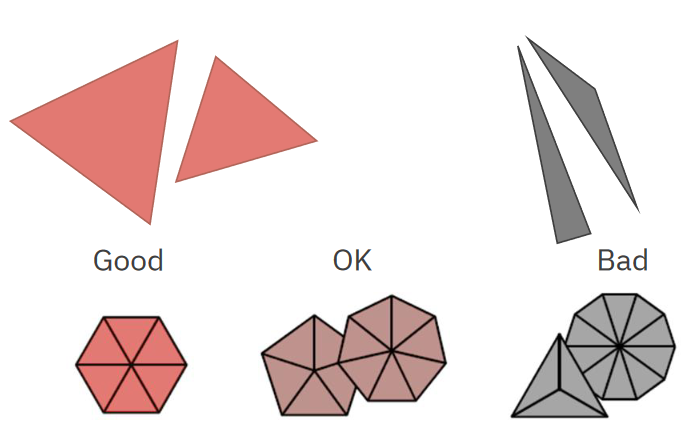
Globální upráva s cílem zlepšit kvalitu meshe, např.: tvar trojúhelníků a četnost vertexů. pa010-2021
Isotropic remeshing
Algoritmus pro regularizaci meshů. Opakuje čtyři kroky:
1. Rozděl hrany delší než 4 / 3 průměrné délky.
2. Zhruť hrany kratší než 4 / 5 průměrné délky.
3. Překlop hrany, pokud to zlepší stupeň vrcholu (ideální je 6).
4. Vycentruj vrcholy.
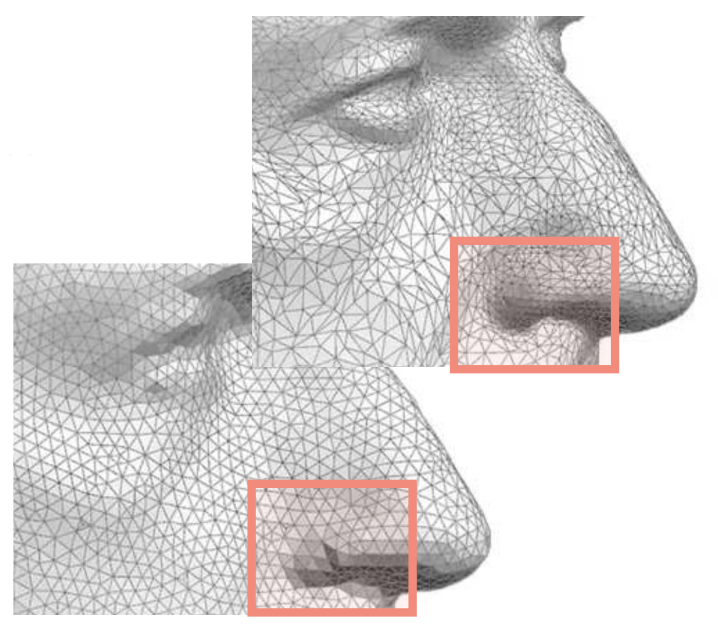
Zlepšuje rychlost některých algoritmů, eliminuje podlouhlé trojúhelníky, které se blbě renderují, zlepšuje subdivision, ale nejde použít vždy a může vést ke ztrátě detailů (řeší Adaptive remeshing). pa010-2021

Implicitní reprezentace a modelování

Když máme objekt definovaný polévkou matematických symbolů místo hromádky trojúhelníků. Jinými slovy máme jednu nebo více reálných funkcí, které klasifikují body v prostoru.

Rovina
Dána bodem p a normálou N, ohraničuje poloprostor. Vzdálenost bodu od roviny je dána (za předpokladu, že N je normalizovaná):
```
f(x) = (x - p) \cdot N
```
Kvadriky / kvadratické plochy
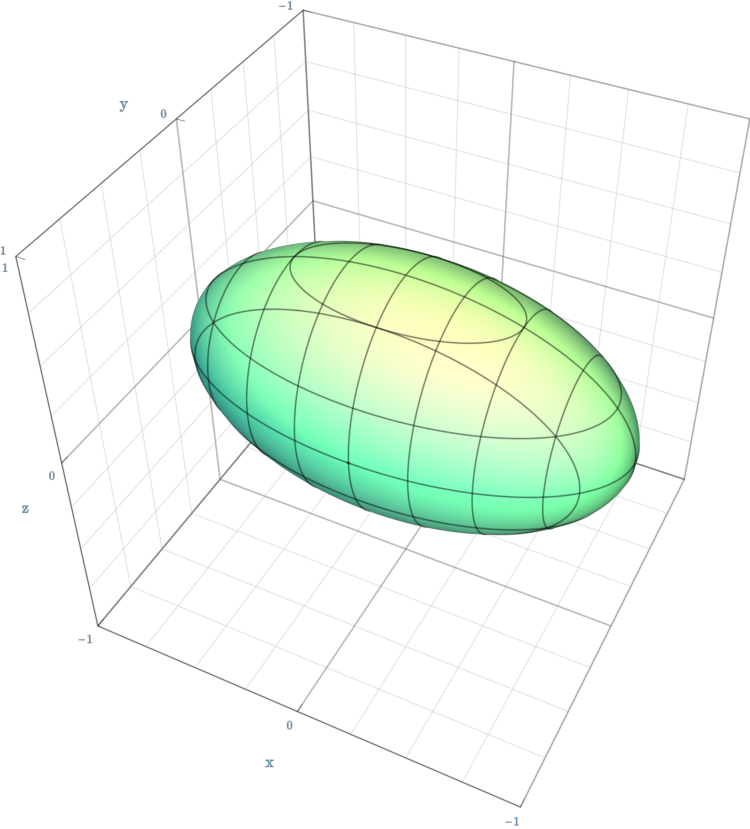
- Elipsoid (třeba koule): \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1,
  
  An ellipsoid by Sam Derbyshire
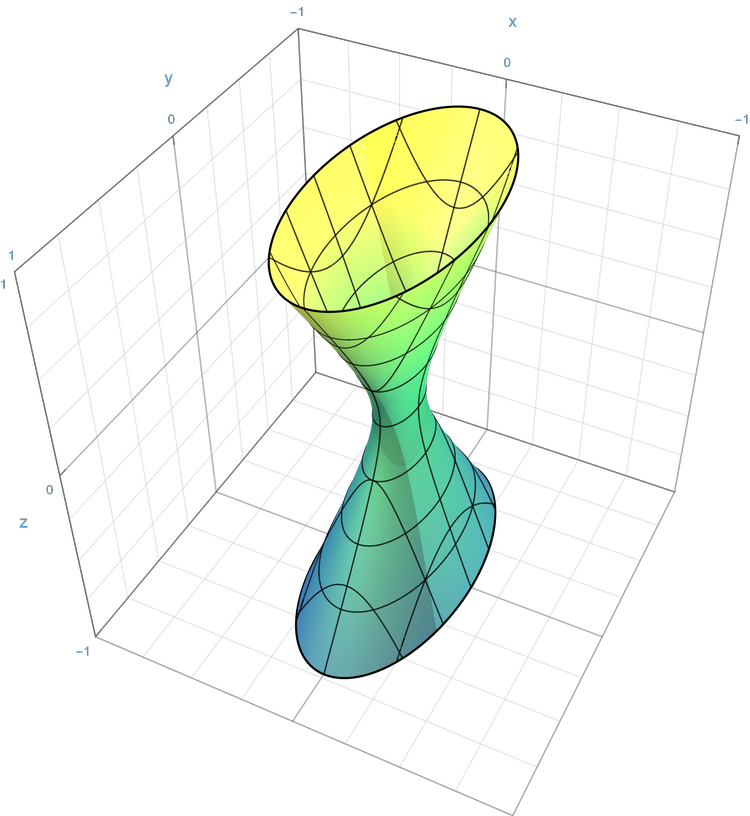
- Hyperboloid (třeba kužel): \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1,
  
  A one-sheeted hyperboloid by Sam Derbyshire
- Válec (cylinder): \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1,
  
  A cylinder by Sam Derbyshire
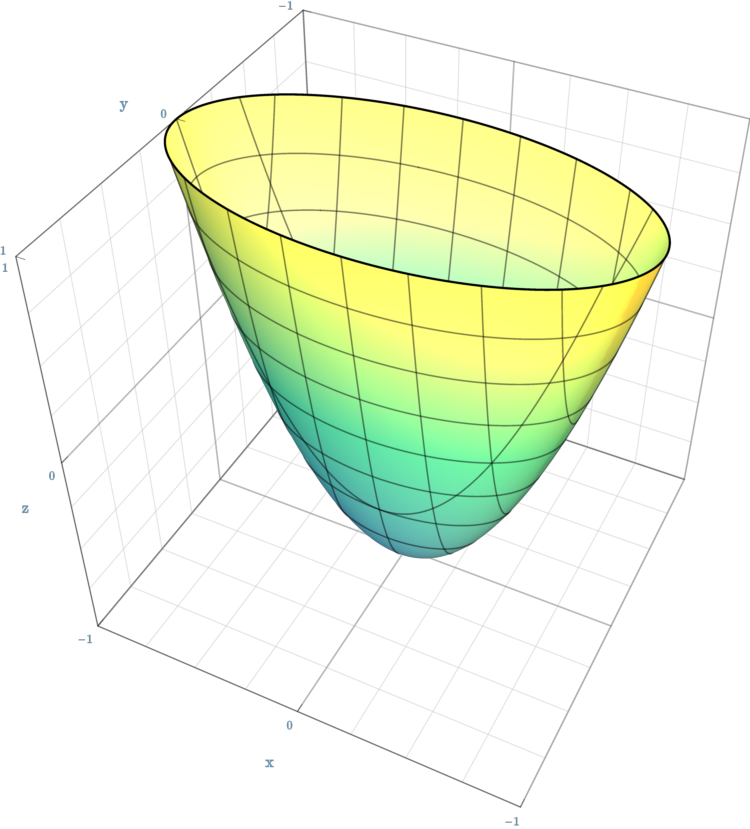
- Paraboloid (třeba miska): \frac{x^2}{a^2} + \frac{y^2}{b^2} - z = 0,
  
  A paraboloid by Sam Derbyshire
Kvartiky / kvartické plochy
- Torus (donut): \left( \sqrt{x^2 + y^2} - R \right)^2 + z^2 - r^2 = 0.
  
  A torus
Distance surfaces
Tělesa lze definovat pomocí vzdálenosti od jiných entit:
- Sphere: d(x, \text{point}) = r,
- Cylinder / capsule: d(x, \text{line}) = r,
- Torus: d(x, \text{circle}) = r,
- Generalized cylinder: d(x, \text{curve}) = r,
- Offset surface: d(x, \text{surface}) = r.
kde d(x, A) je nejmenší vzdálenost bodu x od entity A. pa010-2020
Constructive solid geometry (CSG)
Umožňuje kombinovat implicitní objekty pomocí logických operací. Předpokládáme, že pokud f(x, y, z) < 0 pak je bod uvnitř objektu daném f. Tato metoda nezachovává C^1 spojitost. Pro dva objekty f a g: pa010-2020
- Sjednocení: \min(f, g),
- Průnik: \max(f, g),
- Rozdíl: \max(f, -g).
- Komplement: -f.

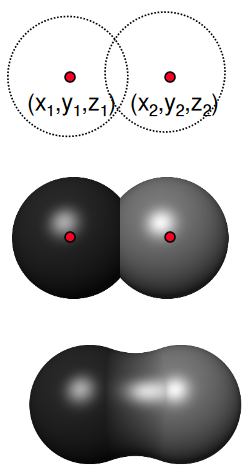
Bloby (kapky)
Součet několika Gaussových křivek. pa010-2020

\begin{align*}

r_i^2 (x,y,z) &= (x-x_i)^2 + (y-y_i)^2 + (z-z_i)^2 \\
f(x,y,z) &= -1 + \sum_i \exp \left( -B_i \cdot \frac{r_i^2 (x,y,z)}{R_i^2} + B_i \right) \\
f(x,y,z) &= -1 + \sum_i D(r_i)

\end{align*}

kde:

B_i je "blobbiness",
R_i je poloměr blobu v klidu,
D(r_i) je Gaussova křivka,
r_i je funkce poloměru kapky.

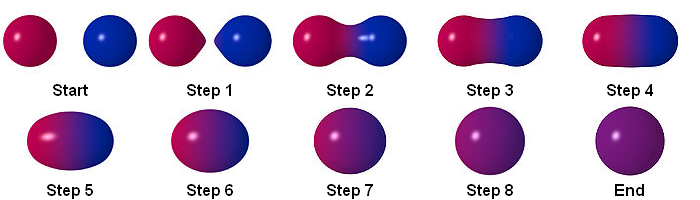
Metaballs
Podobné blobům, ale nepoužívá exponenciální funkci. Organicky se "slévající" koule. pa010-2020

\begin{align*}

D(r_i)= \begin{cases}

\alpha \left( 1 - \frac{3r_i^2}{R_i^2} \right)
    & 0 \leq r_i \leq R_i/3 \\

\frac{3\alpha}{2} \left( 1 - \frac{r_i}{R_i} \right) ^2
    & R_i/3 \leq r_i \leq R_i  \\

0
    & R_i \leq r_i

\end{cases}

\end{align*}

Metaballs by SharkD

Zdroje

[pa010-2021,1] Byška, Furmanová, Kozlíková, Trtík: PA010 Intermediate Computer Graphics (podzim 2021)
[pa010-2020,2] Sochor: PA010 Intermediate Computer Graphics (podzim 2020)
[notes-pa010,3] Moje poznámky z PA010 (podzim 2020)
[manifold-wiki,4] Wikipedia: Topological manifold
[klein-bottle,5] Konrad Polthier: Imaging maths - Inside the Klein bottle
[genus,6] Saul Schleimer: Notes on the complex of curves
[topology, 7] Topology vs. Geometry
[boundaries, 8] Ian Stroud: Boundary Representation Modelling Techniques
[rbo, 9] Interior, Exterior and Closure
[validity,10] Representational validity of boundary representation models
[denoising,11] Bilateral Normal Filtering for Mesh Denoising

18 KiB Raw Blame History