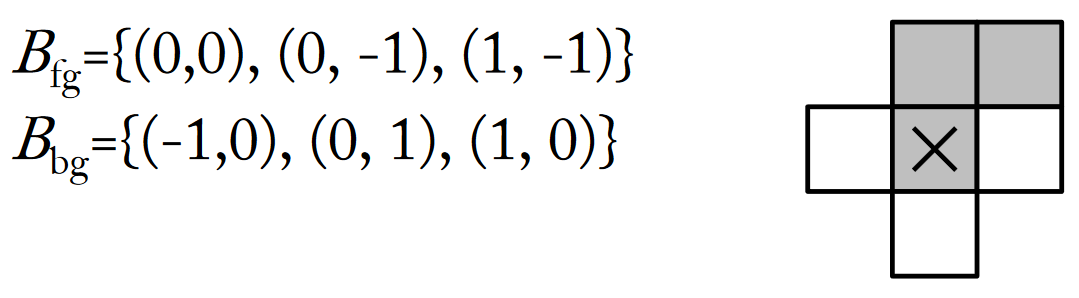21 KiB
| title | description |
|---|---|
| Analýza rastrového obrazu | TODO |
Note
Segmentace obrazu, algoritmy značení komponent, popis objektů, klasifikace objektů. Výpočet mapy vzdáleností. Základy matematické morfologie (dilatace a eroze, otevření a uzavření, hit-or-miss, top-hat, watershed).
PB130/PV131
- Typické fáze analýzy obrazu
- Předzpracování
- Potlačení šumu, odstranění nerovnoměrného osvětlení, atd.
- Segmentace
- Rozdělení obrazu na oblasti odpovídající objektům.
- Popis
- Určení vlastností objektů. Vlastnosti potřebujeme pro klasifikaci.
- Klasifikace
- Rozdělení objektů do tříd podle jejich vlastností.
- Porozumění
- Pochopení smyslu objektů v obraze.
- Předzpracování
Segmentace obrazu
Rozdělení definičního oboru obrazu \Omega na segmenty \Omega = \Omega_0 \cup \Omega_1 \cup \dots \cup \Omega_{n-1} (oblasti, regiony, spojené množiny) podle nějaké společné vlastnosti.
- Regions should be uniform and homogeneous with respect to some characteristic(s).
- Adjacent regions should have significant differences with respect to the characteristic on which they are uniform.
- Region interiors should be simple and without holes.
- Boundaries should be simple, not ragged, and be spatially accurate.
— Haralick a Shapiro
Segmentace přiřazuje každému pixelu obrazu jednoznačnou značku (číslo) podle toho, do které komponenty patří. Výsledkem je šedotónový obraz, kde každá komponenta má jinou intenzitu. Oblasti (=regiony) lze reprezentovat pomocí obrysu (=kontury).
Typickým problémem je rozpoznávání objektů. Možnosti řešení:
- Prahování (často s využitím histogramu)
- Shlukovací metody
- Metody založené na kompresi
- Narůstání regionů (region-growing, split-and-merge)
- PDE-based (parametrické a implicitní aktivní křivky)
- Variační přístupy (modely Mumford-Shah a Chan-Vese)
- Grafové přístupy (graph-cuts, MST, MRF)
- Algoritmus záplava (watershed)
- Hierarchické segmentace
- Metody pracující s modelem tvaru (ASM, AAM)
- Neuronové sítě (zejména konvoluční)
Před samotnou segmentací je vhodné obraz předpřipravit.
-
Algoritmy značení komponent / connected-component labeling (CCL)
Algoritmy, které přiřazují každému pixelu obrazu jednoznačnou značku (číslo) podle toho, do které komponenty patří. Je algoritmickou aplikací teorie grafů na obraz.Obraz je převeden na graf, kde každý pixel je vrchol a hrany jsou mezi sousedními pixely. Hrany jsou ohodnoceny podle podobnosti sousedních pixelů. Segmenty jsou pak komponenty souvislosti v grafu.
Important
Segmentace je problém nalezení oblastí. CCL je jen jedno z možných řešení.
Neuronové sítě
Moderní přístup, vyžaduje velké množství parametrů a mohou být náročné na trénování, existuje mnoho předtrénovaných modelů.
Plně konvoluční sítě -- Všechny vrstvy jsou konvoluční, typicky Downsample + Upsample. Výstupy můžou být různé podle natrénované sítě.
Prahování / thresholding
Prahuje se v Prahe často? Badumtsss
Pixely jsou rozděleny na regiony podle jejich intenzity. Pixely s intenzitou nižší než threshold / práh jsou označeny jako pozadí, ostatní jako popředí.
Důležitá je volba prahu. Někdy víme procento pixelů, které mají být popředí / pozadí, ale typicky zjistíme z analýzy histogramu.
- Prahování je jedna z nejjednodušších metod segmentace obrazu.
- Práh lze určit manuálně nebo automaticky.
Globální prahování
Práh je stejný pro celý obraz. Nezávisle na pozici.
-
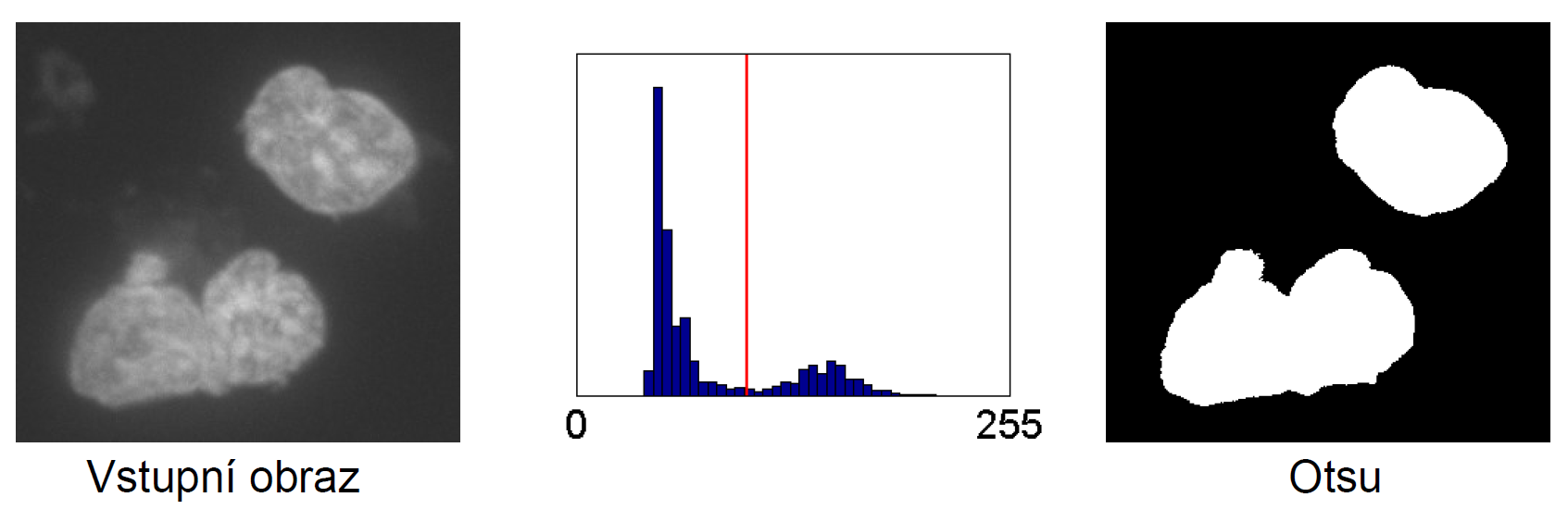
Otsuova metoda
Minimalizace váženého součtu rozptylu intenzit v popředí a pozadí.\sigma^2_w(t) = q_1(t) \sigma_1^2(t) + q_2(t) \sigma_2^2(t)Při velkém šumu je problém s analýzou i segmentací
-
Gradientní prahování
Práh počítaný jako vážený průměr intenzit, kde váhy odpovídají normalizované velikosti gradientu. Vychází z předpokladu, že gradient má velkou velikost v místech výskytu hran => vyšší váha.a_{th} = \sum_{u,v} I(u,v) \cdot \frac{|\nabla I(u,v)|}{\sum_{i,j} |\nabla I(i,j)|} -
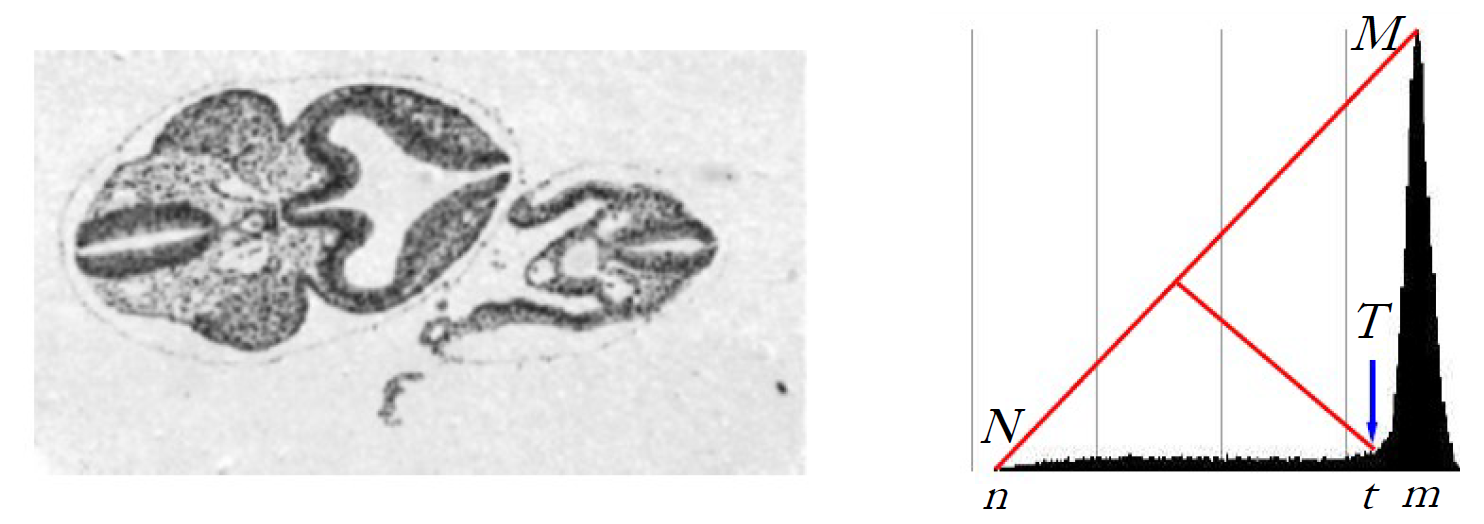
Unimodální histogram
Pro obrazy, kde je viditelné jediné výrazné maximum (pro pixely pozadí). Použijeme Trojúhelníkovou metodu:;\begin{aligned} M &\equiv [m, h(m)] &\text{ globální maximum histogramu}\\ N &\equiv [n, h(n)] &\text{ kde } n \text{ je hodnota intenzity s nenulovou četností nejdál od } m\\ T &\equiv [t, h(t)] &\text{ bod s největší vzdáleností od přímky } MN \end{aligned} -
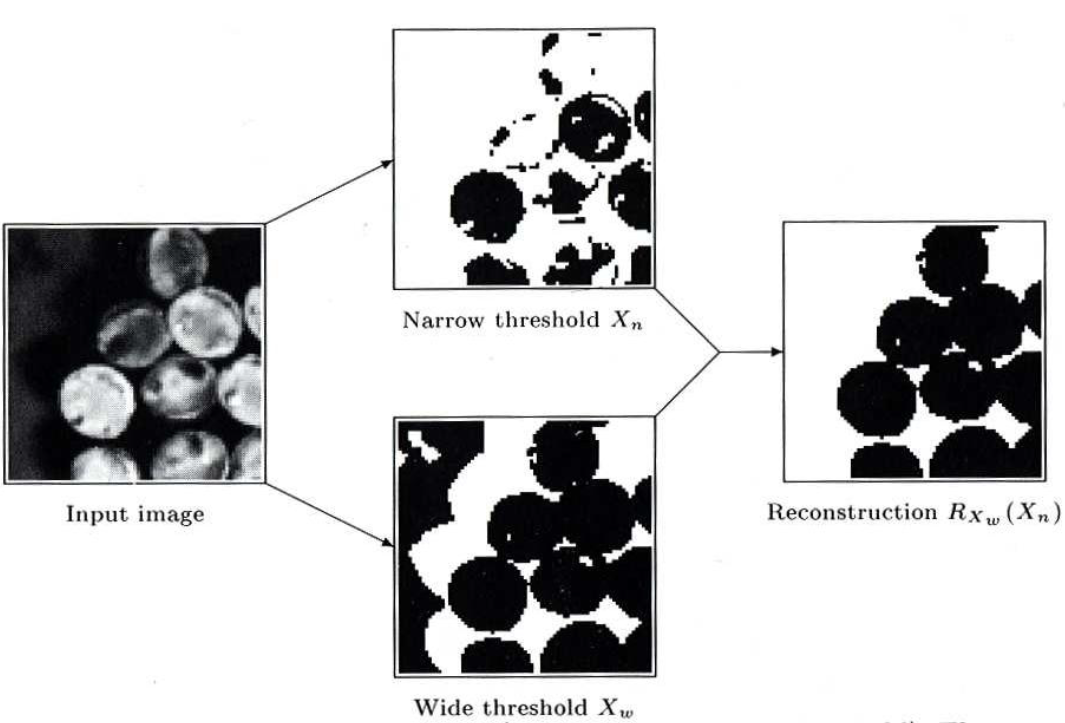
Hysterézní prahování
Používá dva prahy: nízký a vysoký. S pixely mezi nimi zachází vcelku inteligentně.- Pixely s hodnotou vyšší než vysoký práh jsou označeny jako popředí.
- Pixely s hodnotou vyšší než nízký práh jsou oznaženy jako popředí, pokud obsahují alespoň jeden pixel získaný vysokým prahem.
- Všechny ostatní pixely jsou označeny jako pozadí.
-
Víceúrovňové prahování
Pokud je obraz jednoduchá, pak histogram obsahuje více vysokých vrcholů s údolím mezi nimi. Práh lze potom snadno zvolit jako dno těchto údolí.
Lokální (adaptivní) prahování
Práh se mění podle pozice v obraze. Třeba podle průměru intenzit v okolí.
Algoritmus záplava (watershed)
Přístup k segmentaci obrazu z matematické morfologie, který kombinuje segmentaci pomocí narůstání oblastí a segmentaci založenou na hranách.
Detaily jsou popsány dále v textu.
Popis objektů
Popis objektů je proces, při kterém se počítají vlastnosti segmentovaných objektů. Tyto vlastnosti jsou později použity pro klasifikaci objektů nebo hledání podobných objektů v databázi (třeba pro face recognition).
-
Popisovač / descriptor
Funkce, která přiřazuje oblasti obrazu -- objektu -- popis vlastnosti.- Preferujeme deskriptory, které jsou invariantní vzhledem k posunu, rotaci, změně měřítka, změně osvětlení, atd.
- Existují standardizované sady deskriptorů, např. MPEG-7.
Descriptory dělíme na:
- Globální: popisují celý obraz.
- Lokální: extrahují zajímavý rysy z malé části obrazu.
- Třeba rohy, lokální struktury, atd.
- Není potřeba segmentace.
- Objektové: popisují objekt.
- Třeba barva, textura, tvar, atd.
- Potřebujeme segmentaci.
-
Číselné charakteristiky intentizity
Průměr, rozptyl, medián, kvantily, maximum, atd. přes intenzity pixelů objektu. -
Velikost / plocha
Počet pixelů objektu. -
Obvod
Počet hraničních pixelů objektu. -
Topologické vlastnosti
Vlastnosti objektu nezávislé na jeho deformaci. Např. počet děr.Important
Pro topologické vlastnosti viz otázka 3D modelování a datové struktury.
-
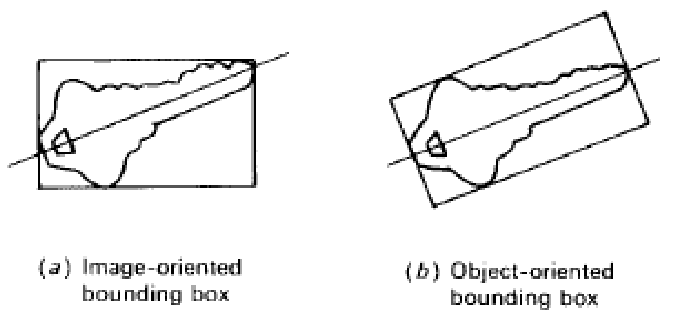
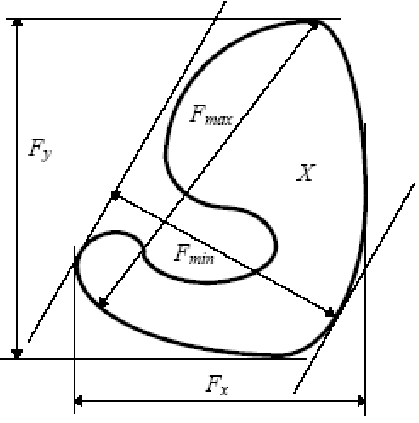
Ohraničující obdélník / bounding box
Nejmenší obdélník ohraničující objekt. -
Průměr / diameter
Velikost objektu. Dá se odhadnout z bounding boxu. -
Kruhovost / circularity
Jak moc je objekt podobný kruhu?\text{circularity} = 4 \cdot \pi \cdot \text{area} / (\text{perimeter} \cdot \text{perimeter}) -
Konvexní obal / convex hull
Nejmenší konvexní polygon ohraničující objekt. -
Hranice / boundary
Popisuje okraj objektu. Obvykle je zakódovaná jako posloupnost bodů. -
Geometrický střed / centroid
Průměr souřadnic pixelů objektu. -
Těžiště / hmotný střed / center of mass
Vážený průměr souřadnic pixelů objektu. Váhy jsou intenzity pixelů. Pokud je objekt homogenní, je těžiště totožné s geometrickým středem. -
Momenty / moments
Popisují tvar objektu. Používájí se ale i pro popis pravděpodobnostních rozdělení.Moment se obecně řídí vzorcem
m_{pq}(R) = \sum_{(u,v) \in R} I(u,v) \cdot u^p v^q, kdeI(u,v)je intenzita pixelu na pozici(u,v)aRje oblast objektu.Vidíme, že obsah odpovídá
m_{00}a geometrický střed (=těžiště)(m_{10}/m_{00}, m_{01}/m_{00}).Můžeme využít centrální momenty, které jsou posunuté do těžiště objektu
m_{pq}(R) = \sum_{(u,v) \in R} I(u,v) \cdot (u - \hat{x})^p \cdot (v - \hat{y})^q- První moment: střední hodnota / hmotný střed.
- Druhý moment: rozptyl / moment setrvačnosti.
-
Moment setrvačnosti / moment of inertia
Míra setrvačnosti při otáčení kolem těžiště. Popisuje rozložení hmoty okolo těžiště (odchylku od něj v jistém smyslu). Umožňuje určit směr nejdůležitější osy objektu. 1Provazochodci využívají moment setrvačnosti při chůzi po laně.
Tip
"Moment" nereferuje na čas, ale spíš na svůj starý význam "důležitost". Ve fyzice navíc obvykle souvisí s otáčivým pohybem. 2
-
Prostorová orientace / spatial orientation
Směr a velikost delší strany nejmenšího bounding boxu. Lze ji také spočítat pomocí momentů setrvačnosti. -
Podlouhlost / elongatedness / eccentricity
Poměr mezi délkou a šířkou objektu. Dá se spočítat pomocí momentů setrvačnosti. -
Matice součásného výskytu / co-occurrence matrix
Matice, která popisuje, jak často se vyskytují dvojice pixelů s danými intenzitami v dané vzdálenosti a směru. Používá se pro popis textury. -
Lokální binární vzory / local binary patterns
Popisují texturu. Základní myšlenka spočívá v nahrazení pixelu 8-bitovým číslem, které udává výsledek porovnání dané hodnoty s hodnotami v osmi-okolí. Je invariantní vůči jasu a byl rozšířen i na rotační nezávislost.
Klasifikace objektů
Problém zařazení objektů do jedné z předem daných tříd.
Important
Detaily přístupů řešení klasifikace lze nalézt v otázce Strojové učení.
-
Konstrukce formálního popisu / známý algoritmus
Pokud lze napsat formální popis tříd, lze klasifikátor realizovat přímo pomocí programu.Takový formální popis může mít podobu např. konečného automatu, gramatiky, predikátových formulí, atd.
-
Učení pod dohledem / supervised learning
Program se nejprve vytrénuje na už oklasifikované množině dat. Poté se použije na nová data. Patří sem např.:- Neuronové sítě.
- Support vector machines.
-
Učení bez dohledu / unsupervised learning
Program se sám naučí rozpoznávat třídy. Patří sem např.:- Hierarchické shlukování.
- K-means clustering.
- Self-organizing maps.
-
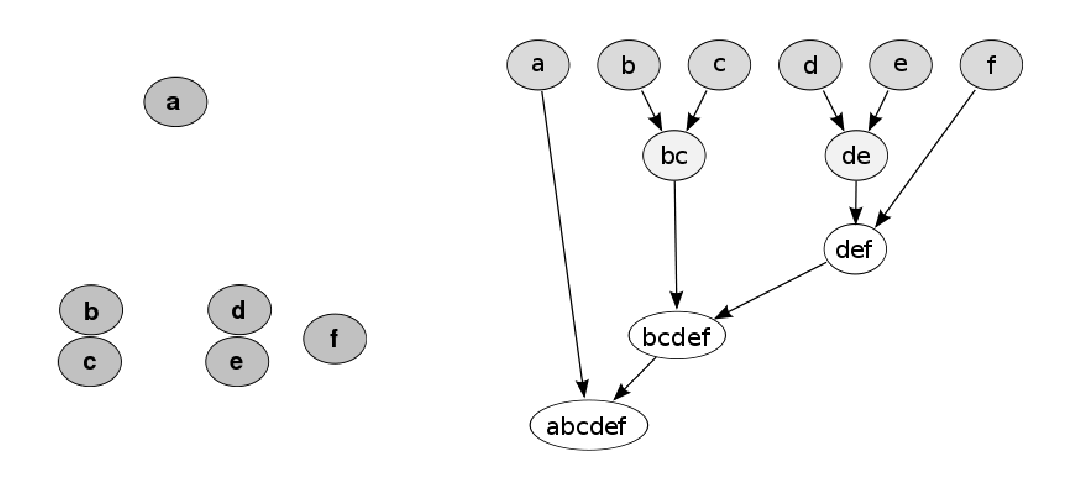
Hierarchické shlukování / hierarchical clustering
Shlukuje objekty podle konektivity.- Každý objekt je jeden shluk.
- Opakovaně spojujeme dva nejbližší shluky.
-
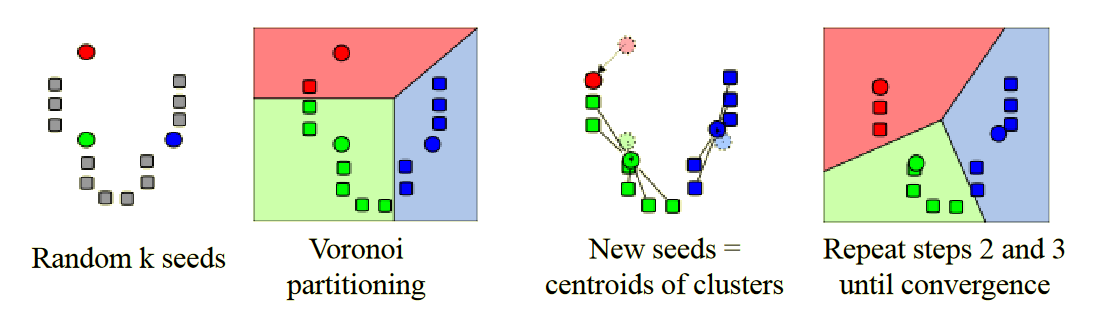
K-means clustering
Shlukuje objekty podle těžišť. Počet shluků je pevně stanovený nak.
Kvalita klasifikace
-
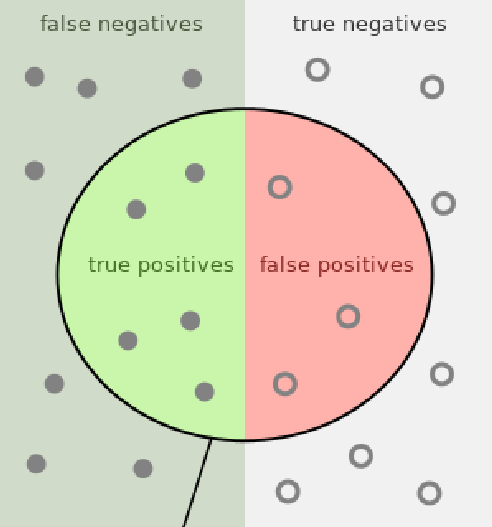
Typ výsledku
- True positive (TP): klasifikátor říká, že objekt do třídy patří, a je to tak.
- True negative (TN): klasifikátor říká, že objekt do třídy nepatří, a je to tak.
- False positive (FP): klasifikátor říká, že objekt do třídy patří, ale je to blbost.
- False negative (FN): klasifikátor říká, že objekt do třídy nepatří, ale je to blbost.
-
Precision
\frac{TP}{TP + FP} -
Sensitivity / recall
\frac{TP}{TP + FN} -
Specificity
\frac{TN}{TN + FP} -
Accuracy
\frac{TP + TN}{TP + TN + FP + FN} -
Ground truth (GT)
Informace o které víme, že je pravdivá. Její získání se liší problém od problému:- Není známa, je dána odborníky.
- Velmi subjektivní, proto se může zapojit více odborníků. Výsledky jsou sločeny hlasováním.
- Je známa, určena z předchozích znalostí.
- Získavají se z předchozích měření, nebo získané z jiných zdrojů.
- Standardizované testovací objekty, fantomy lidských orgánů, atd.
- Je známa přesně a úplně pro velký soubor dat.
- Vstupní objekty i jejich obrázky jsou simulovány.
- Digitální fantomy.
Pomocí GT lze ověřit:
- Výsledky segmentace
- GT udává správnou binární masku. Kvalitu segmentačního algoritmu lze měřit pomocí korelačních koeficientů jako je Dice, Jaccard, atd.
- Výsledky měření: plocha, objem, atd.
- GT udává správné hodnoty měřených parametrů. Chyba je dána rozdílem mezi výsledkem a GT.
- Výsledky klasifikace
- GT udává správné třídy. Kvalitu určujeme na základě poměrů TP, TN, FP, FN.
- Statistické výsledky
- GT udává míru výskytu (v procentech) pro každou třídu. Přesnost měříme srovnáním s GT.
- Není známa, je dána odborníky.
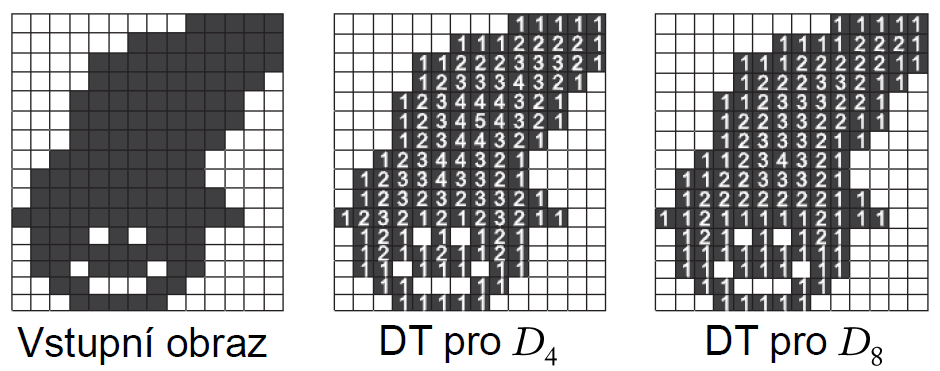
Mapa vzdáleností
Mapování, které každému pixelu popředí přiřazuje vzdálenost k nejbližšímu pixelu pozadí. Používá se třeba pro:
- Oddělení dotýkajících se objektů.
- Výpočet morfologických operátorů.
- Výpočet geometrických reprezentací a měr: kostra, Voroného diagram, osy souměrnosti, atd.
- Navigace robotů.
- Porovnávání vzorů.
-
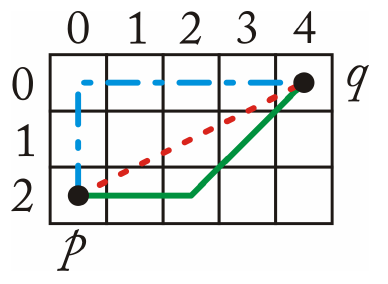
Metriky vzdálenosti
- Euklidovská
\textcolor{red}{D_E}. - Taxikářská
\textcolor{blue}{D_4}. - Šachovnicová
\textcolor{green}{D_8}.
\begin{aligned} \textcolor{red}{D_E}(\lbrack x_1, y_1 \rbrack, \lbrack x_2, y_2 \rbrack ) &= \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \\ \textcolor{blue}{D_4}(\lbrack x_1, y_1 \rbrack, \lbrack x_2, y_2 \rbrack ) &= |x_2-x_1| + |y_2-y_1| \\ \textcolor{green}{D_8}(\lbrack x_1, y_1 \rbrack, \lbrack x_2, y_2 \rbrack ) &= \max(|x_2-x_1|, |y_2-y_1|) \end{aligned} - Euklidovská
Matematická morfologie
Teorie a techniky pro analýzu geometrických struktur. Jsou založené na teorii množin, topologii, atd. Nejčastěji se aplikuje na digitální binární obrazy, ale dá se použít na grafy, meshe, apod. 3
-
Binární obraz
Dá se vnímat jako funkceI: \Omega \rightarrow \{0, 1\}, kde\Omega \sub \mathbb{Z}^2.Ale taky to je množina
F = \{ (x, y) | I(x, y) = 1 \}
Základní operátory
Pracují na každém pixelu a jeho okolí -- strukturním elementu.
-
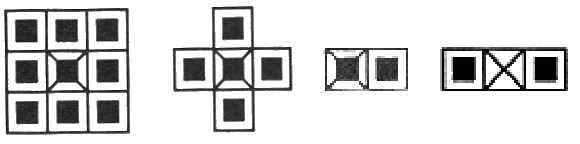
Strukturní element / structuring element (SE)
Množina souřadnic, pomocí které je obraz zpracováván. 4- Má definovaný počátek --
(0, 0). Schematicky se značí křížkem. - Aktuálně uvažovaná souřadnice do něj nemusí patřit.
- Má definovaný počátek --
-
Posunutí množiny
NechťFje množina souřadnic. PosunutíFo vektorbje množina:F_b = \{ s | s = s' + b, s' \in F \} -
Zrcadlení SE
Překlopení souřadnic podle počátku.\breve{B} = \{ (-x, -y) | (x, y) \in B \} -
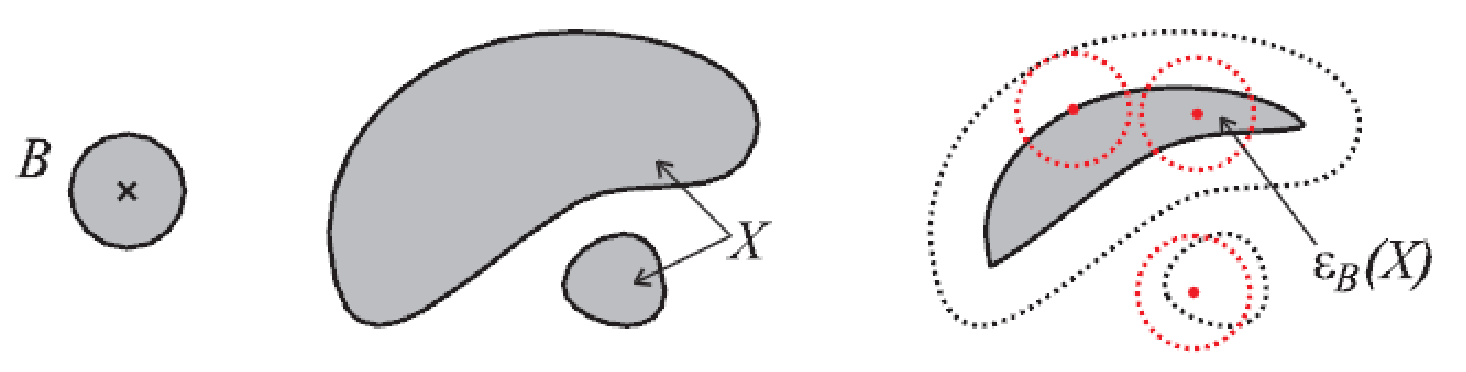
Eroze
Vejde se celý SE do obrazu na dané pozici? Pokud ano, ulož pozici.
Množina bodů takových, že SE posunutý tak, aby počátek odpovídal danému bodu, musí celý patřit do vyšetřované množiny.
\Large \varepsilon_B (X) = \{ x | B_x \subseteq X \}kde
Bje SE aXje vyšetřovaná množina / obraz."Hloupý" algoritmus: hledání minima v okolí daném SE.
-
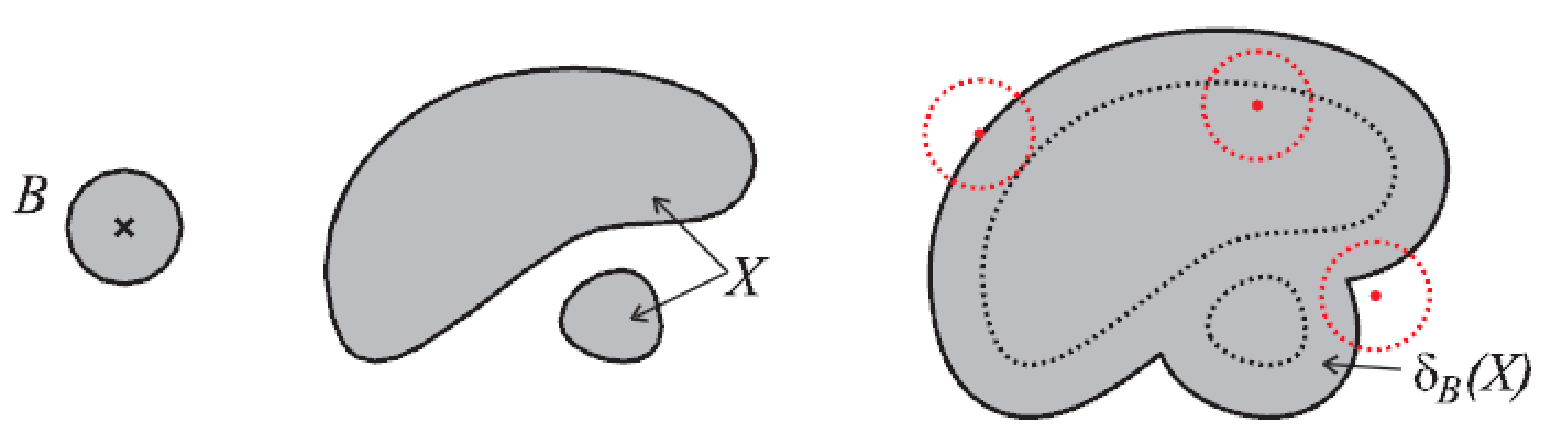
Dilatace
Zasáhne SE vyšetřovanou množinu při umístění na dané pozici? Pokud ano, ulož pozici.
Množina bodů takových, že SE posunutý tak, aby počátek odpovídal danému bodu, aspoň částečně zasáhne vyšetřovanou množinu.
\Large \delta_B (X) = \{ x | B_x \cap X \neq \emptyset \}kde
Bje SE aXje vyšetřovaná množina / obraz."Hloupý" algoritmus: hledání maxima v okolí daném SE.
-
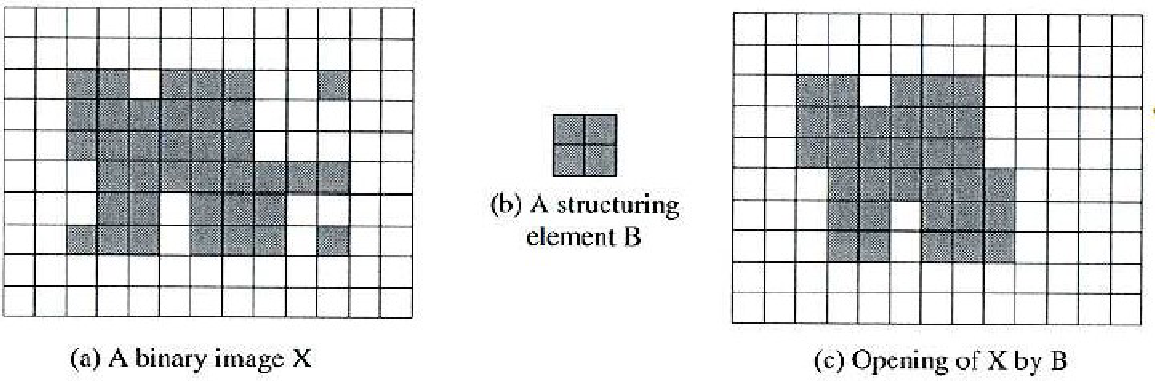
Otevření / opening
Vejde se celý SE do vyšetřované množiny na dané pozici? Pokud ano, tak jej celý ulož na tuto pozici.
Snaha o obnovu obrazu po jeho erozi. Je to eroze a pak dilatace s překlopeným SE.
- Nezávisí na počátku SE.
- Odstraňuje jednotlivá lokální maxima, tenké čáry a rozděluje objekty spojené úzkou cestou.
\Large \begin{aligned} \gamma_B (X) &= \delta_{\breve{B}} (\varepsilon_B (X)) \\ \gamma_B (X) &= \{ B_x | B_x \sube X, x \in X \} \\ \end{aligned}kde
Bje SE aXje vyšetřovaná množina / obraz. -
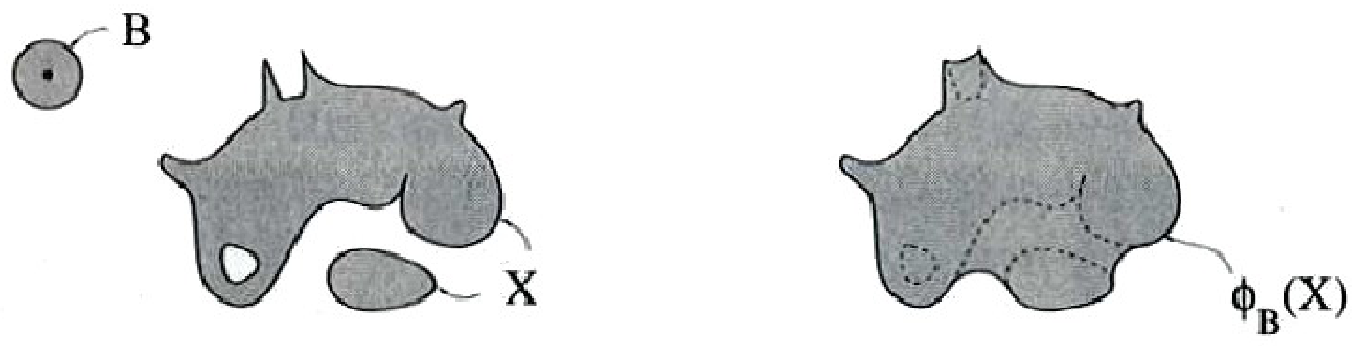
Uzavření / closing
Vejde se SE do pozadí vyšetřované množiny? Pokud ano, tak jej celý ulož do komplementu výsledku.
Snaha o obnovu obrazu po jeho dilataci. Je to dilatace a pak eroze s překlopeným SE.
- Nezávisí na počátku SE.
- Spojuje husté aglomerace lokálních maxim dohromady, vyplňuje malé dírky a vyhlazuje hranice.
\Large \begin{aligned} \theta_B (X) &= \varepsilon_{\breve{B}} (\delta_B (X)) \\ \theta_B (X) &= \left\lbrack \bigcup_{x \in X} B_x \sube X^c \right\rbrack^c \end{aligned}kde
Bje SE aXje vyšetřovaná množina / obraz.
Pokročilejší-ish operace
-
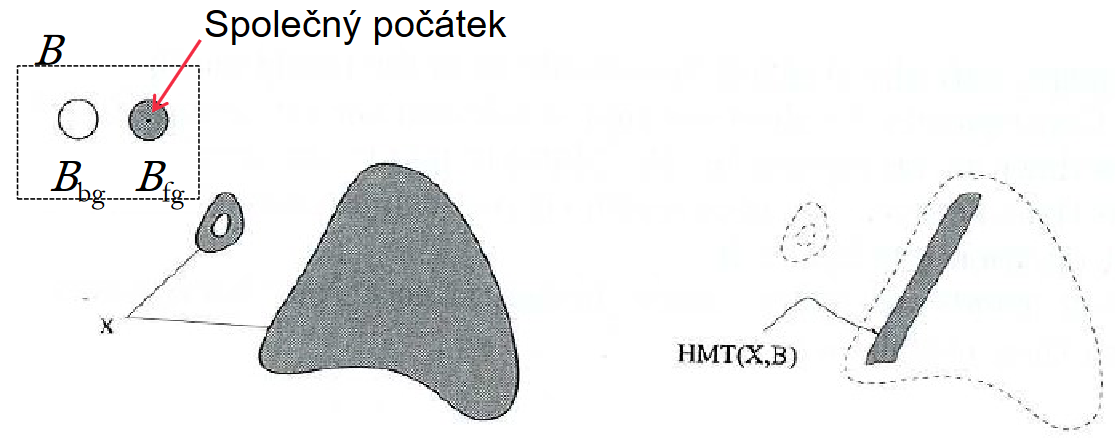
Hit-or-miss
Mějme SE složený ze dvou disjunktních množin. Jedna z nich odpovídá pozadí, druhá objektu / popředí.\Large B = (B_\text{fg}, B_\text{bg}), B_\text{fg} \cap B_\text{bg} = \emptysetVejde se první část SE do vyšetřované množiny na dané pozici a současně druhá část SE ji zcela mine? Pokud ano, tak ulož tuto pozici
\Large \text{HMT}_B(X) = \{ x | (B_\text{fg})_s \sube X, (B_\text{bg})_s \sube X^c \}Používá se k:
- Nalezení instancí konkrétní konfigure pixelů. Například izolovaných pixelů, které jen tak chillují uprostřed ničeho.
- Vytváření kostry / skeletonizing: body kosty mají stejnou vzdálenost od hranice objektu.
- Ztenčování / thinning: převod objektů bez děr na čáry; objektů s dírami na uzavřené smyčky.
- Scvrkávání / shrinking: převod objektů bez děr na izolované body poblíž jejich těžiště; objektů s dírami na uzavřené smyčky.
-
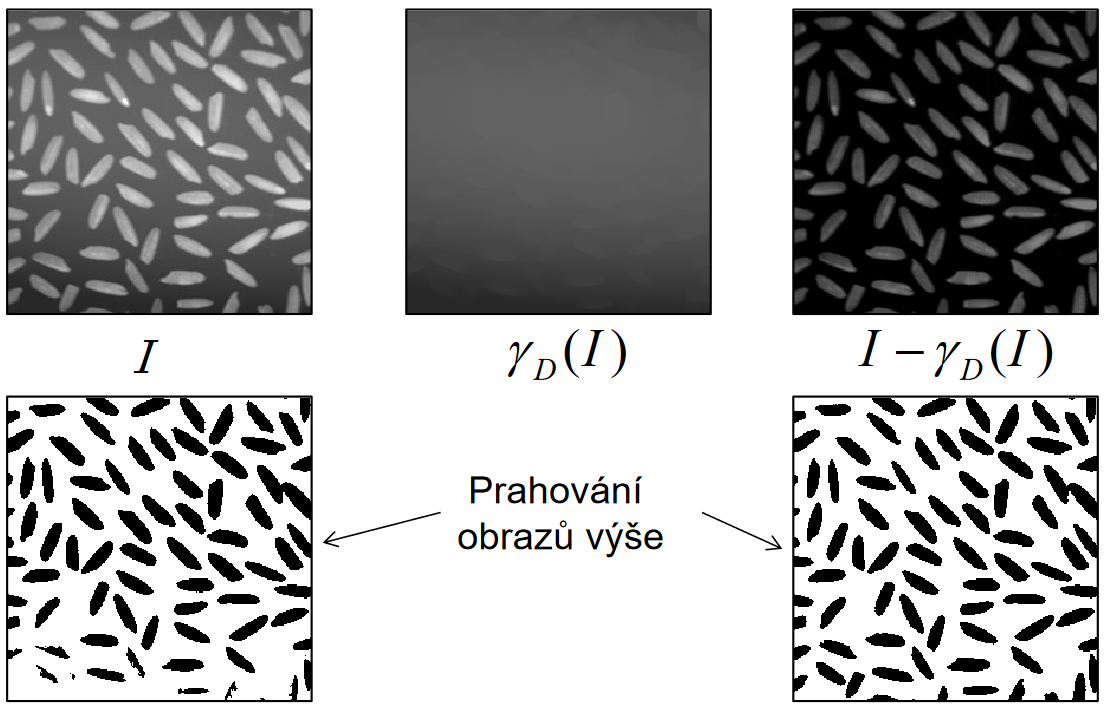
Top-hat transformace
Morfologické transformace obrazu užitečné např. pro korekci nerovnoměrného osvětlení.- Bílý top-hat: rozdíl mezi vstupním obrazem a jeho otevřením.
- Extrahuje světlé skvrny (lokální maxima) nezávisle na jejich intenzitě, bere v úvahu pouze tvar.
- Černý top-hat: rozdíl mezi uzavřením a vstupním obrazem.
- Extrahuje tmavé skvrny (lokální minima) nezávisle na jejich intenzitě, bere v úvahu pouze tvar.
- Bílý top-hat: rozdíl mezi vstupním obrazem a jeho otevřením.
-
Watershed
Algoritmický přístup k segmentaci skrze matematickou morfologii. Kombinuje segmentaci narůstáním oblastí a detekcí hran. 4- Simulace zvyšování hladiny vody krok za krokem.
- Obraz vnímán jako topografický povrch. Ve všech lokálních minimech je "udělána díra" odkud stoupá hladina vody.
- Postupně zvyšujeme hladinu za vzniku bazénů / catchment basins.
- Když už by se měly dva bazény spojit, zabráníme tomu postavením hrází.
- Hráze tvoří čáry rozvodí / watershed lines.
Postup:
- Vyhlaď obrázek např. pomocí Gaussova filtru.
- Zjisti maximální a minimální intenzitu obrazu:
(a_\text{high}, a_\text{low}). - Urči značky pro budoucí objekty (manuálně nebo z lokálních minim).
- Inicializuj binární obraz
Bvynulováním. - Pro
aoda_\text{low}doa_\text{high}:- Nech narůst oblasti značek, tak aby byly do
Bpřidány pixely s intenzitou\leq a. - Nedovol spojení oblastí různých značek.
- Nech narůst oblasti značek, tak aby byly do
Bnyní definuje oblasti objektů. Počet objektů je roven počtu značek.
Další zdroje
- Haralick, Shapiro: Image segmentation techniques
- Zhang, Fritts, Goldman: Image segmentation evaluation: A survey of unsupervised methods
- What is the reasoning behind using "moment" in the "moment of inertia"?