fi-notes/VPH01_pokrocila_grafika.md at f3a6fd9c7db98ff80a120faede522976e0a4da6d

Vojtěch Struhár f3a6fd9c7d Transform callouts to GH flavor

2025-06-07 00:22:34 +02:00

19 KiB

Raw Blame History

title	description
Pokročilá počítačová grafika (2023)	TODO

Warning

Tato je stará verze otázky. Nová verze: Grafické principy ve vývoji her.

Note

Techniky aproximace objektů. Renderování objemových dat (bodový mrak, techniky rekonstrukce povrchů, přímé renderování objemu). Lokální a globální modely nasvícení. Renderování založené na fyzikálních modelech (PBR). Techniky renderování stínů.
PA010, PA213

Techniky aproximace objektů

3D objekty mohou být definované mnoha miliony polygony či výpočetně náročnými matematickými funkcemi. Pro renderování v reálném čase je tedy žádoucí je zjednodušit a přitom zachovat jejich vzhled -- aproximovat je.

Important

Aproximace objektů souvisí s collidery, kterým se částečně věnuje otázka Grafické a fyzikální principy.

Redukce počtu polygonů

Slučování polygonů (merging) či odstranění polygonů (culling), které nejsou vidět. pa010-2021

Variational Shape Approximation
1. Cluster surface elements (e.g. triangles) into k regions.
  - Start with random seed.
  - Apply region growing based on proximity, orientation, etc.
  - Refine seeds (find best representatives) and repeat until regions stabilize.
2. Fit each region into a proxy (e.g. plane) with minimum error.
  - E.g. by using a weighted average of triangle normals.
Iterative Decimation -- Edge Collapse Simplification
1. Přiřaď každé hraně cenu (třeba quadratic error metric -- suma vzdáleností bodu od rovin)
2. Zbab se hrany s nejnižší cenou sloučením jejích vrcholů.
3. Opakuj, dokud nemáš požadovaný počet polygonů.

Implicitní reprezentace

Pokud dokážeme model vyjádřit pomocí matematických funkcí, nemusíme ukládat polygonovou síť. Např. koule je definována jako x^2 + y^2 + z^2 = r^2. Šetří prostor, plyne z ní však nutnost výpočtu. Ne všechny modely je možné takto vyjádřit jednoduše.

Constructive solid geometry (CSG)
Dokáže reprezentovat komplexní objekty jako kombinace primitiv (krychle, koule, válec, ...). Tyto primitiva jsou následně transformována (posun, rotace, škálování) a kombinována (sjednocení, průnik, rozdíl).

Šetří místo, ale je náročnější na výpočetní výkon než polygonová síť.

Zjednodušení vzhledu

Nemusíme zjednodušovat jen povrch/objem modelu, ale i související atributy. Můžeme snížit rozlišení textur, či snížit počet barev v paletě. Pokud používáme PBR, můžeme upravit parametry materiálu nebo použít jednodušší model osvětlení.

Bounding Volume Hierarchies (BVH)

Hierarchie bounding volumes -- jednoduchých objektů jako jsou kostky, koule, apod. -- které obsahují nějakou část objektu / geometrie scény. Používá se k rychlým průchodům scénou, např. při detekci kolizí, ray tracingu, atd. Svým způsobem jde tím pádem také o aproximaci objektů.

Discrete Oriented Polytopes (DOP)
Generaliace bounding boxu. k-DOP je konvexní polytop -- generalizace mnohoúhelníků ve 2D, mnohostěnů ve 3D atd. -- který vzniká průnikem k bounding slabů -- prostorů mezi dvě paralelními rovinami daných osou a vzdáleností mezi rovinami. Použitých os může být více než je dimenze prostoru. Např. 3D scéna může mít 13-DOP.

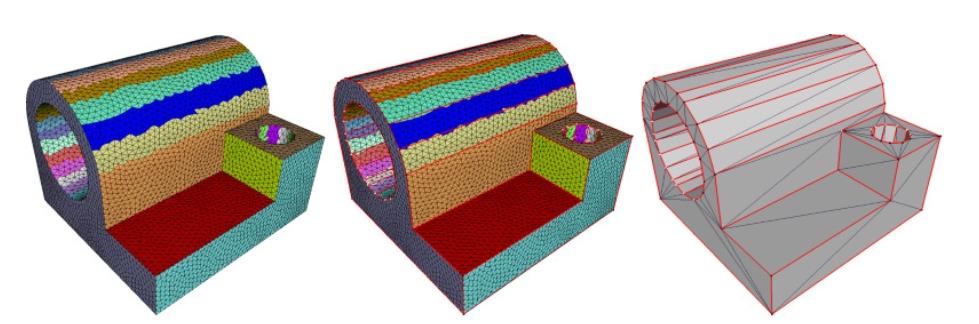
Renderování objemových dat

Voxel
Voxel je 3D analogií pixelu -- bod v prostoru, který má určitou hodnotu (např. barvu, intenzitu, ...). Voxelová data mohou být získána (např. pomocí CT, MRI, PET, atd.) nebo být také výsledkem simulace (např. simulace proudění tekutin).
Objemová data

Objemová data jsou definována nejčastěji jako mřížka voxelů.

Při renderování objemů je třeba vyřešit několik souvisejících problémů s daty:
- Data s neuniformním vzorkem.
- Chybějící data.
- Šum a outlieři.
Kromě pozic mohou surová data obsahovat také normály, barvy, apod.

Bodový mrak (point cloud)

Množina bodů v prostoru, které nemají žádnou strukturu. Nejjednodušší přístup k renderování objemu, kdy se nepokoušíme o žádnou rekonstrukci povrchu. Body však mohou mít různé barvy a průhlednost.

Rekonstrukce povrchu

Ze získaných dat se snažíme vytvořit mesh. Ten lze vyrenderovat tradičním způsobem.

Marching cubes
Rozděluje prostor na mřížku voxelů. V každém voxelu se pak vyhodnocuje, zda je povrch objektu překročen. Pokud ano, je třeba přidat triangle mesh pro daný voxel. pa010-2020 marching-cubes

Marching cubes by Ryoshoru
Marching tetrahedra
Analogický k marching cubes, ale používá místo krychlí čtyřstěny. Řeší problém s některými nejednoznačnými konfiguracemi v marching cubes, a taky nikdy nebyl patentován (kdežto marching cubes ano). marching-tetrahedra
Vertex clustering
Metoda podobná iterative decimation (viz výše), nejprve vytvoříme clustery bodů, poté pro každý vybereme vhodného reprezentanta (např. průměrem, mediánem, quadric error minimization, atd.), pak už jen zbývá mesh "sešít" např. pomocí triangulace. pa010-2020
Dual contouring
Z voxelů se stanou vrcholy (tedy využíváme dualního grafu). Tyto vrcholy jsou ale posunuty tak, že povrch může obsahovat jak ostré hrany tak zaoblené plochy. dual-contouring
Delaunay triangulation
Vytváří trojúhelníkovou síť, tak že žádný bod se nenáchází ve vepsané kružnici žádného trojúhelníku. Maximalizuje nejmenší úhel trojúhelníků. delaunay-triangulation

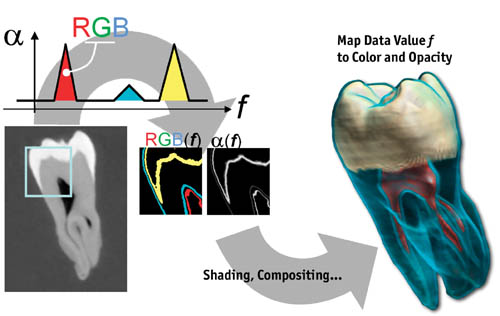
Direct volume rendering (přímé renderování objemu)

Nerekonstruujeme povrch, ale mapujeme data na optické vlastnosti jako je barva a průhlednost. Během renderování se pak využívá path tracing, a tyto vlastnosti se akumulují podél jednotlivých paprsků. gpugems

V realitě tohle chování paprsku popisujeme integrály. V počítačové grafice se ale využívá aproximace pomocí sumy.

The Process of Volume Rendering gpugems

Emmission-absorption model
Paprsek vstupuje do objemu, kde je absorbován a emitován. Výsledná barva je pak výsledkem akumulace těchto vlastností. V notaci používáme: pa213
- \kappa je funkce absorpce,
- q je emise.
Optická hloubka / optical depth
Bezrozměrná veličina \tau, která popisuje, jak moc jde "vidět skrz" něco, třeba plyn. Čím větší, tím méně vidíme.

Z jiné perspektivy je to akumulovaná absorpce na paprsku. Optická hloubka mezi dvěma body s_1 a s_2 na paprsku je dána jako:
```
\tau(s_1, s_2) = \int_{s_1}^{s_2} \kappa(s) ds
```
Průhlednost / transparency
Průhlednost popisuje, jak dobře vidíme skrz objem. Upadá exponenciálně s růstem optické hloubky.

Průhlednost mezi dvěma body s_1 a s_2 na paprsku je dána jako:
```
\theta(s_1, s_2) = e^{-\tau(s_1, s_2)}
```
Volume rendering integral
Intenzitu světla I v místě paprsku s počítáme pomocí: pa213
```
\begin{aligned}

I(s) &= I(s_0) \cdot \theta(s_0, s) + \int_{s_0}^s q(s') \cdot \theta(s', s) ds' \\

&= I(s_0) \cdot e^{-\tau(s_0, s)} + \int_{s_0}^s q(s') \cdot e^{-\tau(s', s)} ds'

\end{aligned}
```
kde:
- s_0 je místo, kde se paprsek dostal dovnitř nějakého světlo-vyzařujícího objemu,
- I(s_0) je boundary light, tedy světlo na hranici objemu,
- q(s') je emise v bodě s'.
Back-to-front
Přístup k počítání I, kdy paprsky vyhodnocujeme od hranice objemu dále od kamery směrem ke kaměře.

Výhoda je, že nemusíme udržovat proměnnou pro průhlednost. Nevyhoda je, že musíme vyhodnotit všechny voxely v cestě paprsku, protože "přepisují" výsledek.
Front-to-back
Přístup k počítání I, kdy paprsky vyhodnocujeme od hranice objemu blíže ke kameře směrem od kamery.

Dá se utnout dřív, když víme jistě, že už je výsledek neprůhledný a tedy už se nic nezmění.
Transfer function
Funkce T, která mapuje hodnoty voxelů na barvu a průhlednost. Klasifikuje voxely. pa213

Modely nasvícení (illumination models)

Lokální osvětlení (local illumination) / direct lighting
Berou v úvahu jen světlo, které dopadá přímo na daný bod/objekt. Neřeší okolní objekty, ani nepřímé osvětlení. Je založený na empirických znalostech o chování světla, spíš než simulaci fyzikálních zákonů.

Patří sem Blinn-Phong, pomineme-li jeho ambientní složku.
Globální osvětlení (global illumination)
Řeší nejen přímé osvětlení, ale i odrazy, lomy, průhlednost, stíny, atd.
Ambient illumination
Aproximace globálního osvětlení pomocí konstantní ambientní barvy.
Ray tracing
Metoda, kdy simulujeme paprsky světla vycházející ze zdroje světla a dopadající na scénu. Používá se jak k lokální tak globální iluminaci. Počítáme však jen to, co vidí kamera, jelikož posíláme paprsky skrze pixely. Pokud se kamera pohne, musíme znovu paprsky zpravidla počítat znovu.
Radiosity (metoda osvětlení)
Metoda, kdy scénu rozdělíme na segmenty a simulujeme "přelévání" světla mezi segmenty. Je vypočetně náročné, ale nezávisí na pozici a směru kamery.

Physically based rendering (PBR)

Physically based rendering (PBR) je způsob renderování, který se snaží co nejvíce aproximovat realitu pomocí fyzikálních modelů světla, stínů, materiálů, očí, atd. pv227-2022 Aproximuje efekty jako absorpci světla nebo jeho rozptyl pod povrchem objektů.

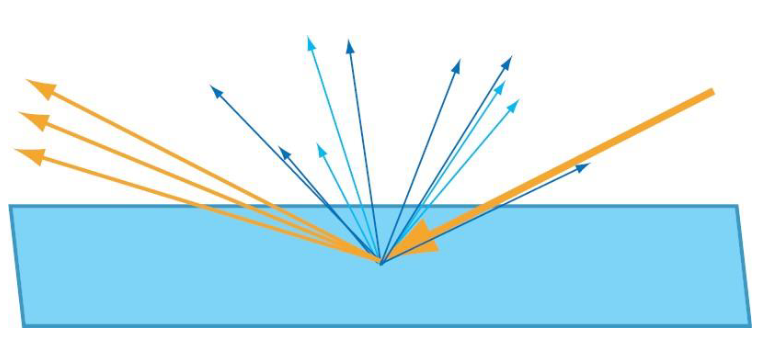
Absorption and scattering / absorpce a rozptyl
Materiály mohou světlo buď absorbovat (v takovém případě jsou alespoň částěčně průhledné) nebo odrážet a rozptylovat (objekty jsou matné). Většina materiálů kombinuje oba efekty. Světlo se může rozpylovat i pod povrchem (subsurface scattering).
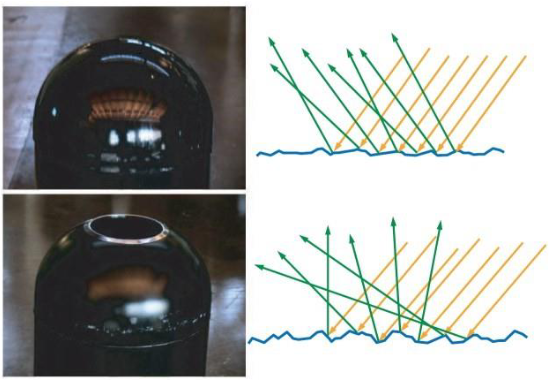
Reflection / odraz světla
V nejjednodušším případě se úhel odrazu rovná úhlu dopadu. V realitě úhel odrazu však záleží na mnoha faktorech jako je i vlnová délka světla. Toto chování popisují Fresnelovy rovnice. Znamená to, že odraz má barvu. V praxi používáme Schlickovu aproximaci:
```
F_\text{Schlick}(F_0, L, N) = F_0 + (1 - F_0) \cdot (1 - L \cdot N)^5
```
kde:
- F_0 je Fresnelův odraz při úhlu 0 (dá se dohledat pro daný materiál),
- L je vektor směru světla,
- N je vektor normály povrchu.
Z určitého úhlu se povrchy, které normálně světlo odráží špatně, jeví jako zrcadla (tanakawho)
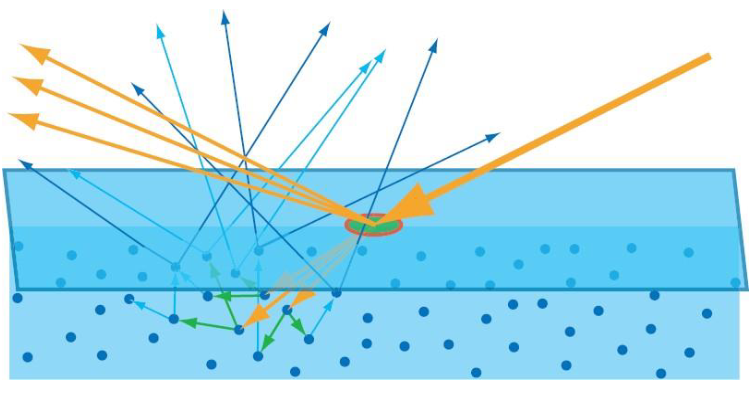
Refraction / lom světla
Kovy světlo absorbují, v homogenních materiálech (např. sklo) pokračuje v jiném směru, a v heterogenních materiálech (např. kůži) se světlo rozptýlí a pak absorbuje. Lom světla popisuje Snellův zákon:
```
\frac{\sin \alpha_1}{\sin \alpha_2} = \frac{v_1}{v_2} = \frac{n_2}{n_1}
```
kde:
- \alpha_1 je úhel dopadu (angle of incidence),
- \alpha_2 je úhel lomu (angle of refraction),
- v_1 je rychlost šíření vlnění ve vnějším prostředí,
- v_2 je rychlost šíření vlnění v prostředí objektu,
- n_1 je index lomu vnějšího prostředí,
- n_2 je index lomu prostředí objektu.
Diffuse lighting
Když všechno (neabsorbované) světlo opustí objekt ze stejného místa, kam dopadlo.
Subsurface scattering
Když neabsorbované světlo opustí objekt z jiného místa, než kam dopadlo.
Microfacets / mikro-plošky
Ne všechny objekty jsou ploché. Většina má nerovnosti, které jsou menší než pixel, ale větší než vlnová délka dopadajícího světla, proto je modelujeme nějakou pravděpodobností distribucí (např. Gaussovou).

Existuje řada modelů chování microfacet, např. Cook-Torrance, Oren-Nayar, Ashnikmin-Shirley, Normalized Blinn-Phong, atd.
Geometrická atenuace
Postupná ztráta "intenzity" paprsku v důsledku geometrie objektu.
- Shadowing -- facety zastiňují jiné facety.
- Masking -- facet nejde vidět, protože ho zastiňuje jiný facet.
- Interreflection -- světlo se odráží mezi facety, než je odraženo zpátky ke kameře.

Fyzikální věličiny radiometrie

Radiant energy / energie záření (Q)
"Energy per one photon."

Jednotka: Joule (J)
Radiant flux, radiant power / zářivý tok (\Phi)
"Energy per second." Bezva na popisování síly světel jako jsou žárovky, plošná světla, atd.
```
\Phi = \frac{\partial Q}{\partial t}
```
Jednotka: Watt (W) = J/s
Irradiance / ozářenost, ozáření (E)
"Flux through area." Světlo dopadající na jednotku plochy. Kvadraticky se zmenšuje s rostoucí vzdáleností od zdroje. Bezva na popis vzdálených zdrojů jako je slunce.
```
E = \frac{\partial \Phi}{\partial A}
```
Jednotka: Watt per square meter (\frac{W}{m^2})
Radiosity / radiozita (radiometrická veličina) (J)
Jako irradiance, ale je to světlo vycházející z jednotky plochy.
Radiance / zář (L)
"Flux through a cone of directions from an area." a nebo "Flux through an area from a cone of directions." Nezmenšuje se se zvětšující se vzdáleností od zdroje. Tohle měří senzory.
```
L = \frac{\partial^2 \Phi}{\partial A_\text{proj} \partial \omega}
```
Jednotka: Watt per square meter per steradian (\frac{W}{m^2 \cdot sr})

Bidirectional Reflectance Distribution Function (BRDF)

Funkce popisující poměr mezi dopajícím a odraženým světlem na povrchu objektu.

f(\vec{l}, \vec{v}) = \frac{\partial L_o(\vec{v})}{\partial E_i(\vec{l})}

Povrch je nasvícen ze směru \vec{l} s ozářením \partial E(\vec{l}). \partial(L_o(\vec{v})) je odražená zář ve směru \vec{v}.

Udává pravděpodobnost, že světlo dopadající na povrch ze směru \vec{l} bude odraženo ve směru \vec{v}.

Z pohledu teorie pravděpodobnosti / statistiky to ale není distribuční funkce ale spíš hustota pravděpodobnosti.

BRDF je řešena pomocí ray tracingu, radiosity, nebo nějakým hybridním řešením.

Techniky renderování stínů

Stíny jsou důležité, jelikož:

zvyšují věrohodnost scény,
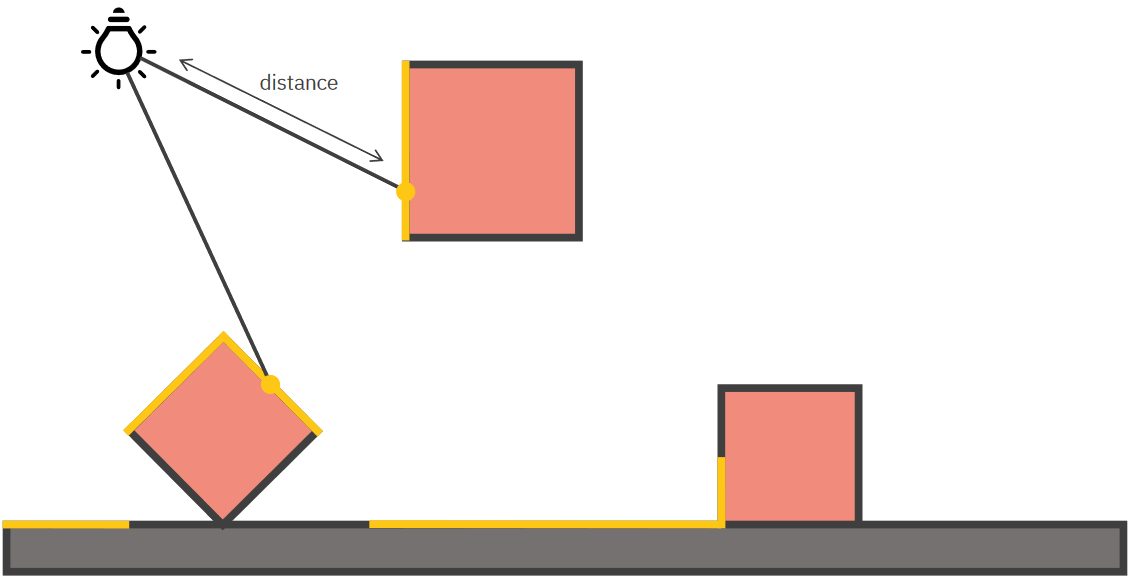
jsou indikátorem vzdálenosti objektů od sebe -- hloubky scény,
mohou dávat informaci o objektech, které jsou mimo zorné pole kamery nebo ukryté za jinými objekty,
popisují tvar objektu, na který jsou promítány.
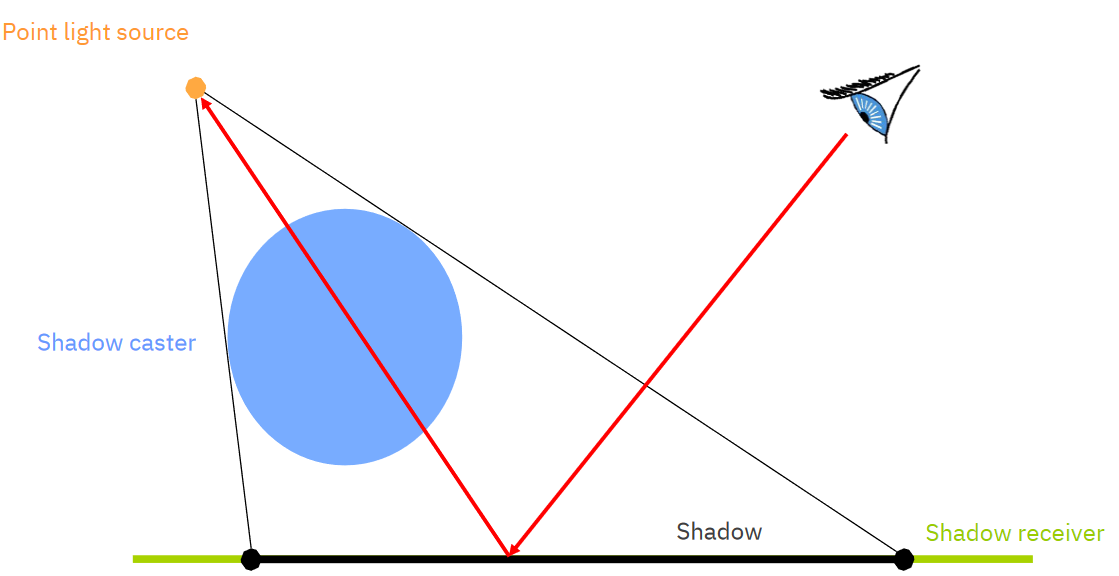
Hard shadows / "ostré" stíny
Rozlišují jen, zda je bod osvětlený nebo ne. Neřeší se, jak moc je osvětlený. Týká se bodových světel.
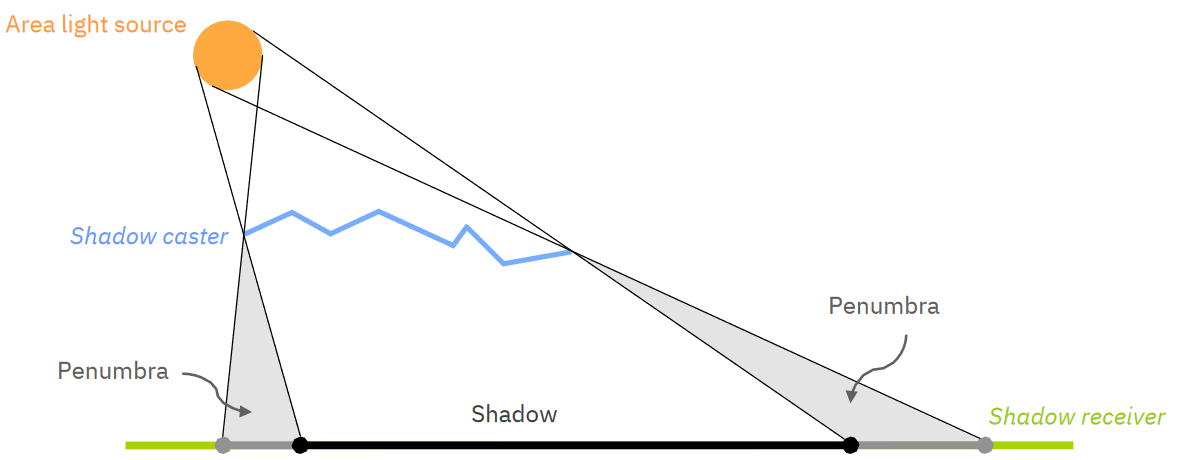
Soft shadows / "měkké" stíny
Rozlišují i částečně osvětlené oblasti. Týká se světel, která mají plochu.
Planar shadows
Vykreslí objekt ještě jednou projektovaný na danou plochu.
- Použitelné na velké plochy jako je rovná podlaha či stěny.
- Blinn (1988)
- Jednoduché a rychlé.
- Nedá se použít na sebevržené stíny, stíny vržené na jiné objekty, kulaté plochy, atd.
Fake shadows and Projective textures
Použitelné pro velice málo velmi velkých dopadových objektů.
1. Vyrenderuj objekt černobíle z pohledu světla a ulož do textury.
2. Projektuj tuhle texturu na každý objekt, na který má dopadat stín.
Shadow maps
Renderuje scénu z pohledu světla, ale ukládá si do textury jen hloubku. Při vykreslování scény z pohledu kamery sampleuje texturu a porovnává vzdálenost od světla s hloubkou v textuře. Pokud je větší, je bod ve stínu.

Important

Shadow mapám se důkladně věnuje otázka Renderování s využitím GPU
Shadow volumes
Počítá stíny ve 3D. Shadow volume explicitně popisuje objem prostoru ve stínu nějakého polygonu.
1. Pro každý shadow caster, vyrob shadow volume.
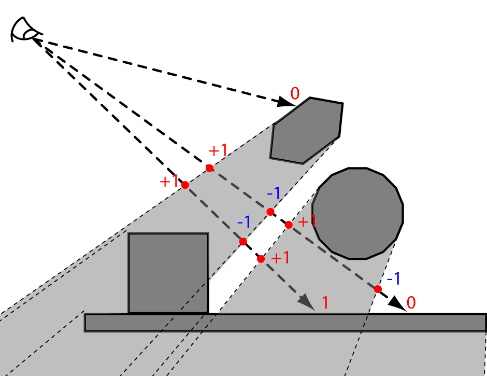
2. Pro každý fragment, počítej do kolika objemů paprsek z kamery do fragmentu vstoupí (+1) a z kolika vystoupí (-1). Pokud je výsledek > 0, pak je fragment ve stínu, pokud je 0 tak je osvětlený.
  
  Prakticky se používá Stencil Buffer Algorithm, kdy renderujeme pro každý objekt nejprve front faces a pak back faces. Tenhle přístup je problematický, pokud je kamera ve stínu, ale řešitelný pokud obrátíme pořádí objektů -- jdeme od nekonečna ke kameře (Z-fail, Carmack’s reverse).
Soft shadows
Existuje množství algoritmů. Například shadow mapy s Percentage Closer Filtering (PCF). Jsou ale výpočetně náročnější než hard shadows.