15 KiB
| title | description |
|---|---|
| Zpracování obrazu pomocí minimalizace energie | TODO |
Note
Variační filtrování. Aktivní křivky a plochy (geodetický model, Chan-Vese model). Minimalizace pomocí grafových řezů. Variační optický tok.
PA166
Variační filtrování
Variační filtrování neřeší lokálně jednotlivé pixely, ale snaží se minimalizovat enetgii celého obrázku.
Typickým předpisem takovéhle funkce je
E_f(u) = \int_{\Omega} ( \underbrace{(u - f)^2}_\text{similarity} + \alpha \underbrace{\Psi (| \nabla u |^2)}_\text{smoothness} ) dx
Chceme, aby byl obrázek co nejpodobnější původnímu (data/similarity term), ale zároveň co nejvíc vyhlazený (smoothness term/regularizer/penaliser). Poměr těchto dvou členů určuje parametr \alpha. Regularizer \Psi určuje “metodu” vyhlazení:
| Tikhonov (linear) -- identita | \Psi(\lvert \nabla u \rvert^2) = \lvert \nabla u \rvert^2 |
| Charbonnier | \Psi(\lvert \nabla u \rvert^2) = 2 \lambda^2 \sqrt{1 + \lvert \nabla u \rvert^2 / \lambda^2} - 2 \lambda^2 |
| Total Variation | \Psi(\lvert \nabla u \rvert^2) = 2\sqrt{\lvert \nabla u \rvert^2} = 2\lvert\nabla u\rvert |
Tuto funkci můžeme minimalizovat dvěma způsoby:
Přímé řešení (lineární funkce)
Provedeme diskretizaci a poté parciálně zderivujeme pro jednotlivé pixely. Tím dostáváme sadu lineárních funkcí položených nule. Tyto poté položíme do matice, kterou řešíme. Matice má hodnoty pouze kolem diagonály, což znamená, že je velmi rychle řešitelná např. pomocí Thomas method.
Pokud je obraz 2D, bereme všechny pixely jako dlouhou 1D posloupnost a řešíme obdobně.
Matice je ale obrovská, proto můžeme využít např. Gauss-Seidel metodu, s pomocí které matici řešíme iterativně po řádcích.
Nelineární řešení
Použijeme Variační kalkulus, který dokáže minimalizovat Funkcionály
- Funkcionál
Bere na vstupu funkci a přiřazuje jí nějakou hodnotuu(x) \Rightarrow \mathbb{R}.
Pro řešení můžeme nyní využít Euler-Lagrangeovy rovnice. Pro funkcionál E_f(u) = \int_{\Omega} ( (u - f)^2 + \alpha \Psi (| \nabla u |^2) ) dxdy získáme předpis pro minimalizaci:
0 = u - f - \alpha \text{div}(\Psi'(\lvert \nabla u \rvert^2) \nabla u)
Nyní můžeme hezky vidět vztah k difuznímu filtrování (otázka PGV10):
| Variační metoda | \frac {u - f}{\alpha} = \text{div}(\Psi'(\lvert \nabla u \rvert^2) \nabla u) |
| Difuzní filtrování | \partial_t u = \text{div}(\Psi'(\lvert \nabla u \rvert^2) \nabla u) |
Přičemž vidíme, že
- Tikhonov regulariser ~ Linear diffusivity
\Psi(\lvert \nabla u \rvert^2) = \lvert \nabla u \rvert^2\Psi'(\lvert \nabla u \rvert^2) = 1
- Charbonnier regulariser ~ Charbonnier diffusivity
\Psi(\lvert \nabla u \rvert^2) = 2 \lambda^2 \sqrt{1 + \lvert \nabla u \rvert^2 / \lambda^2} - 2 \lambda^2\Psi'(\lvert \nabla u \rvert^2) = \frac{1}{\sqrt{1 + \lvert \nabla u \rvert^2 / \lambda^2}}
- Total Variation regulariser ~ Total Variation diffusivity s difusivitou
\frac{1}{\lvert \nabla u \rvert}\Psi(\lvert \nabla u \rvert^2) = 2\lvert\nabla u\rvert\Psi'(\lvert \nabla u \rvert^2) = \frac{1}{\lvert \nabla u \rvert}
Aktivní křivky a plochy
- Segmentace
Chceme rozdělit obrázek podle něčeho (region based, edge based, texture, …) - Segmentace založená na energii
Hledáme konturu s minimální energií. Závisí na volbě iniciální křivky - hledá pouze lokální minimum.
Hadi
Působí dvě energie:
- Vnitřní - tvar a plynulost křivky
- Vnější - omezení z obrázku
Kontura zadaná, jako parametrická křivka p(s): [0, 1] \rightarrow \mathbb{R}\ \ \ \ p(s) = (x(s), y(s))^T. Podobně, jako u variačního filtrování, definujeme funkcionál energie, který se snažíme minimalizovat:
E(p) = \int_0^1 E_{int}(p(s)) + E_{ext}(p(s)) ds
Kde E_{int} je vnitřní energie, kde \alpha a \beta jsou váhy pro délku (\alpha) a křivost (\beta) křivky:
E_{int}(p(s)) = \alpha(s) \lvert p'(s) \rvert^2 + \beta(s) \lvert p''(s) \rvert^2
A E_{ext} je vnější energie, kde P je potenciální funkce:
E_{ext}(p(s)) = P(p(s))
-
Potenciál
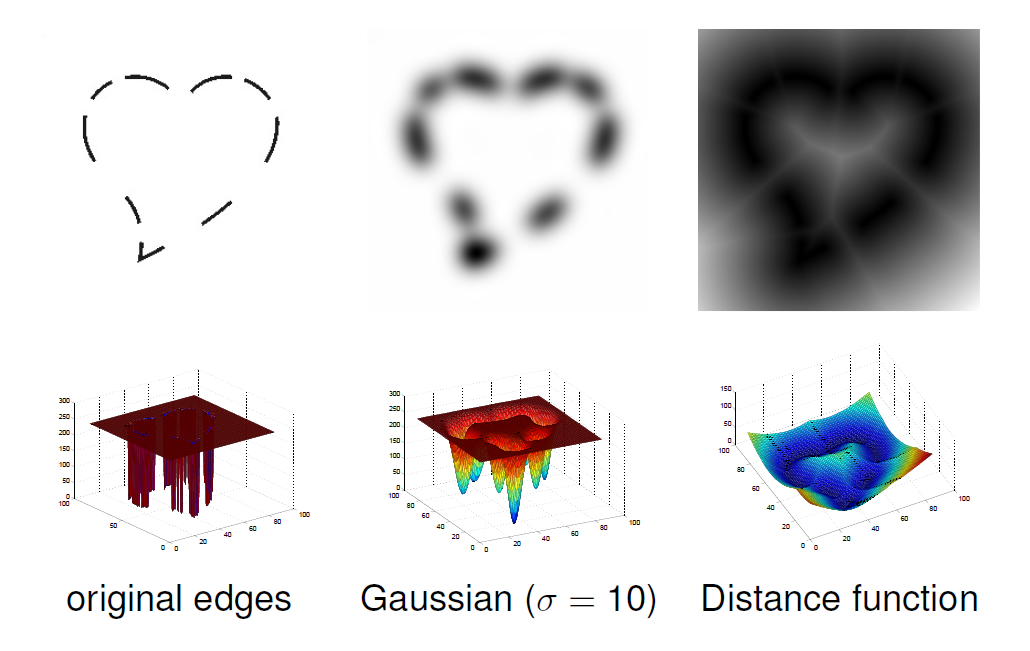
Potenciál určuje vztah křivky k obrázku. Může být definován různými způsoby:- Hrany -
P(x, y) = -\lvert \nabla f(x, y) \rvert^2 - Hrany po rozmazání -
P(x, y) = -\lvert \nabla (G_{\sigma}(x, y) * f(x, y) )\rvert^2 - Linie -
P(x, y) = -f(x, y) - Linie po rozmazání -
P(x, y) = -G_{\sigma}(x, y) * f(x, y)
- Hrany -
Minimalizaci funkcionálu chceme opět udělat Euler-Lagraneovou rovnicí, tedy:
\alpha p''(s) + \beta p'''(s) - \nabla P = 0 \text{, kde } p(0), p'(0), p(1), p'(1) \text{ jsou zadané}.
Na derivace můžeme použít finite differences a přepíšeme výsledek do matice AX = F_{ext}. Blbý ale je, že F*{ext} závisí na p a p závisí na F*{ext}. Proto se to řeší iterativně \frac{\partial p}{\partial t} = F_{int}(p) + F_{ext}(p)\\p(s, 0) = p_0(s)
-
Problémy
-
Reparametrizace
- Body mají tendenci se slévat do míst s nízkou potenciální energií
- Musíme jednou za čas rozmístit body pravidelně podél vzniklé křivky
-
Normalizace (Diskretizace času)
- Velikost gradientu není ničím omezena a může nám “vystřelit” body úplně do kša
- Místo klasického gradientu vezmeme gradient normalizovaný, tedy jen směr
-
Diskretizace prostoru
- Potenciální funkce je spočítaná pouze v diskrétních bodech, ale křivka může procházet i mimo tyto body
- Na dopočítání použijeme například bilineární interpolaci
-
Problémy předchozí detekce hran
-
Balonování
-
Kontury mají tendenci se slévat do středu do jednoho bodu, kde zaniknou
-
Často chceme detekovat něco, kde začneme uvnitř
-
K externím silám přidáme tzv. balonovou sílu ve směru normály křivky
F_{ext} = k_1 n(s) - k \frac{\nabla P}{|\nabla P|} -
Parametr
k_1ovlivňuje, jestli se křivka “nafukuje”, nebo “vyfukuje”, můžeme měnit během iterování
-
-
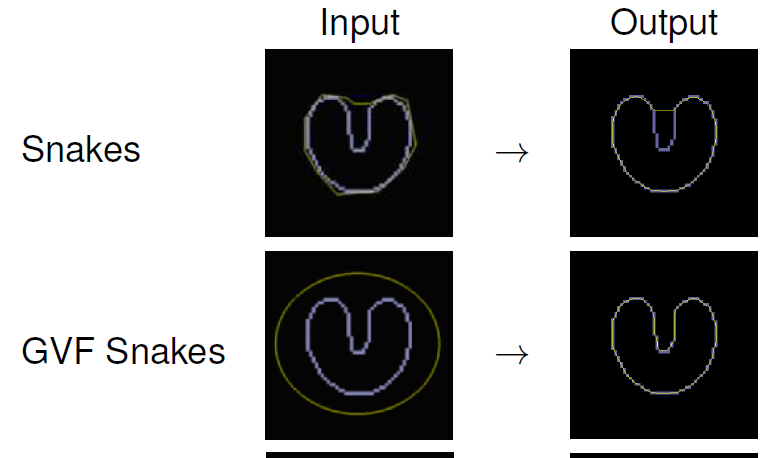
GVF Snakes
-
Kontury mají problém opsat “tvar rohlíku” a nic je nenutí dostávat se do úzkých prostor
-
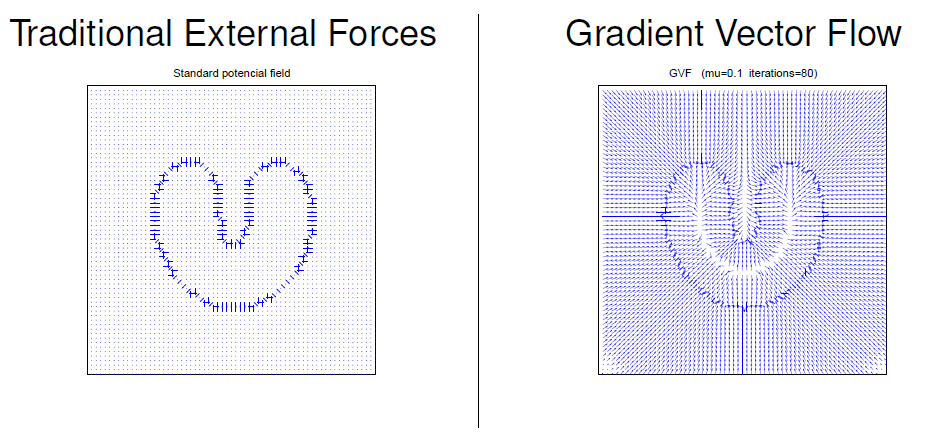
Převedeme externí síly na nové pole sil, kterému říkáme Gradient Vector Flow
-
Chceme v podstatě přidat síly tam, kde nejsou hrany, aby celý prostor k hranám směřoval
Geodetické aktivní křivky
Hloupé na hadech (to, co jsem popisoval doteď) je, že závisí na parametrizaci (rozložení bodů na křivce). GAC naopak na parametrizaci nezávisí.
Pro křivku minimalizujeme funkcionál (Chceme co nejmenší délku křivky && co nejnižší celkový gradient): +
E_{GAC}(C) = \int_0^1 g(\underbrace{\lvert \nabla G_{\sigma} * I(C(q)) \rvert}_{\text{Vyhlazený obrázek}}) \underbrace{\lvert C'(q) \rvert}_{\text{Délka křivky}} dq
Funkce g snižuje vliv délky na energii, pokud leží v místech s vysokým gradientem, protože je nepřímo úměrná rozmazanému gradientu: +
g(\lvert \nabla G_{\sigma} * I(x, y) \rvert) = \frac{1}{1 + \lvert \nabla G_{\sigma} * I(x, y) \rvert}
Chan-Vese model
Do teď jsme neřešili, co je uvnitř kontur (homogenita), jen co je přímo pod nimi. Chan-Vese model se snaží najít konturu, která rozdělí obrázek na dvě části s různými intenzitami.
E_{CV}(\underbrace{C}_{\text{Křivka}}, \underbrace{c_1}_{\substack{\text{Odhad} \\ \text{popředí}}}, \underbrace{c_2}_{\substack{\text{Odhad} \\ \text{pozadí}}}) =
\underbrace{\mu L(C)}_{\text{Délka křivky}} + \underbrace{\lambda_1 \int_{\Omega_1} (f(x) - c_1)^2 dx}_{\text{Odlišnost popředí od odhadu}} + \underbrace{\lambda_2 \int_{\Omega_2} (f(x) - c_2)^2 dx}_{\text{Odlišnost pozadí od odhadu}}
- Regularity term - délka dělící křivky
- Data term (2x) - rozdíl částí (fg,bg;
\Omega_1, \Omega_2) od konstantního odhaduc_1, c_2 - Parametry
\mu, \lambda_1, \lambda_2určují vyhlazení, variabilitu pozadí a popředí respectively - Pro danou křivku C jsou optimální
c_1, c_2s průměrnou hodnotou
Abychom se zbavili integrálů přes část oblasti, můžeme použít Harveside funkci, která vrací 0 pro nulu a 1 jinak. Tím dostaneme:
\begin{aligned}
E_{CV}(C, c_1, c_2) &= \mu \int_{\Omega} \lvert \nabla H (u(x)) \rvert dx &\footnotesize{\text{ Délka křivky}}\\
&+ \lambda_1 \int_{\Omega} (f(x) - c_1)^2 H(u(x)) dx &\footnotesize{\text{ Odlišnost popředí od odhadu}}\\
&+ \lambda_2 \int_{\Omega} (f(x) - c_2)^2 (1 - H(u(x))) dx &\footnotesize{\text{ Odlišnost pozadí od odhadu}}\\
\end{aligned}
Diskretizujeme a řešíme.
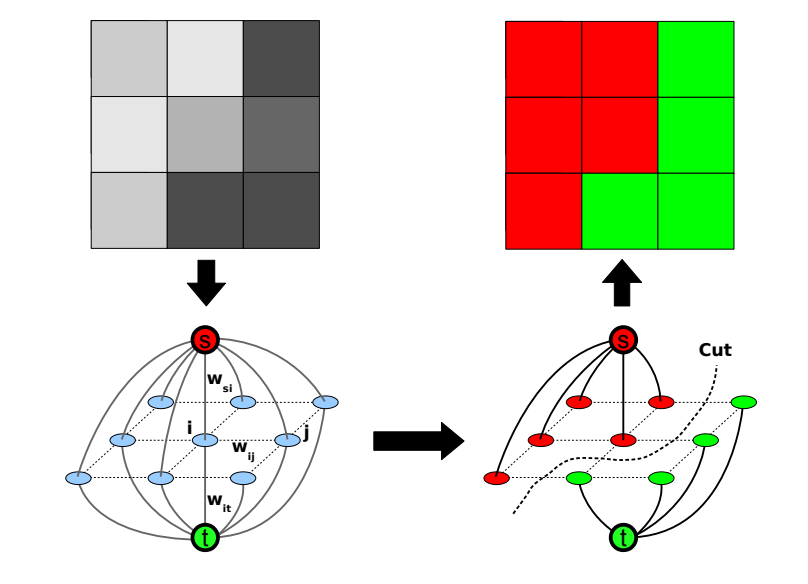
Minimalizace pomocí grafových řezů
Rozdělení metodou minimálního řezu využívá algoritmu pro hledání minimálního řezu v grafech. Uvažme graf, kde každý pixel je jeden vrchol a pro všechny pixely vytvoříme hrany ze zdroje (s) a spotřebiče (t) a hrany mezi sousedy.
-
Riemannovy metrické systémy
Normálně, když počítáme délku mezi dvěma body, počítáme ji, jakod = \sqrt{u^T \cdot u}. Můžeme ale přidat tzv. metrický tensorM, který může tuto délku upravit v závislosti na směrud = \sqrt{u^T \cdot M \cdot u}. Díky tomu potom můžeme měřit nejen euklidovskou vzdálenost, ale třeba:- Euklidovskou vzdálenost -
M = I(identita) - Geodetickou vzdálenost -
M = \text{diag}(g(\lvert \nabla I(\cdot) \rvert)) - Anizotropní vzdálenost -
M = g(\lvert \nabla I(\cdot) \rvert) \cdot E + (1 - g(\lvert \nabla I(\cdot) \rvert)) \cdot u \cdot u^T(kdeu = \frac{\nabla I}{\lvert \nabla I \rvert}jednotkový vektor ve směru gradientu aEje identita)
- Euklidovskou vzdálenost -
Pro aproximaxi vah hran v našem grafu můžeme použít Riemannovu metriku:
w_k^R = w_k^{\epsilon} \cdot \frac{\text{det} M}{(u_k^T \cdot M \cdot u_k)^{p}}
Geodetická segmentace
Můžeme rozdělit obrázek na dvě části pomocí minimálního řezu na dvě části podle geodetické vzdálenosti.
- t-linky (hrany do s nebo do t) - nastavíme váhy na 0 vyjma pixelů s omezením (víme, že jsou popředí, nebo pozadí), které nastavíme na nekonečno (nebo velkou konstantu), čímž zabráníme výběr do minimálního řezu
- n-linky (mezi sousedními pixely) - podle Riemannovy metriky
Chan-Vese pomocí minimálního řezu
Můžeme rozdělit obrázek na dvě části, přičemž o některých pixelech víme, jestli patří do popředí, nebo do pozadí. Podobně, jako u Chan-Vese křivkami máme odhad c_1, c_2 pro popředí a pozadí. Nastavme tedy váhy:
- t-linky -
w_{si} = \lambda_2(f(i) - c_2)^2 \text{, } w_{it} = \lambda_1(f(i) - c_1)^2 - n-linky - podle Riemannovy metriky
Bohužel w_{si}, w_{it} jsou závislé na c_1, c_2. Typicky řešíme tak, že si tipneme, provedeme iteraci, aktualizujeme a jedem znovu
Variační optický tok
Pro sekvenci obrázků f(x,y,t) chceme získat vektor posunutí (u(x,y,t),v(x,y,t))^T každého místa obrázku.
Máme 2 předpoklady, které platí pro všechny metody:
- Zachování jasu (mezi snímky se nám nemění jas obrázku) = BCA -
f(x+u, y+v, t+1)=f(x,y,t)(posunutý pixel se rovná neposunutému) - Malé změny (objekty se posouvají jen o několik málo (třeba 5) pixelů) - Abychom mohli provést linearizaci Taylorovým rozvojem
Z rovnice pro BCA můžeme linearizací dostat
0 = f(x+u, y+v, t+1) - f(x,y,t) \\
\approx f_x(x,y,t)u + f_y(x,y,t)v + f_t(x,y,t)
Tím dostáváme nejdůležitější rovnici linearised optical flow constraint (OFC)
f_x u+f_y v + f_t = 0 (\nabla f \cdot (u,v) + f_t = 0)
Problém Apertury = OFC ukazuje jen tok rovnoběžný s gradientem (protože jinak to není vidět)
Taky protože f_x u+f_y v + f_t = 0 \sim \nabla f \cdot (u,v) + f_t = 0 , tedy máme projekci reálného směru na gradient
-> Nonuniqueness = Můžeme libovolně přidat část toku kolmou na gradient, aniž bychom změnili výsledek
Lukas a Kanade (Lokální metoda)
Přidává 3. předpoklad:
- Zachování jasu
- Malé změny
- Konstantnost toku v okolí
B_\rhokaždého bodu
Chceme minimalizovat následující lokální energii (integrál přes okolí)
E(u,v) = \frac{1}{2} \int_{B_\rho(x_0, y_0)} (f_x u + f_y v + f_t)^2 dx dy
Parciálně zderivujeme a převedeme na matice
\begin{aligned}
0 = \frac{\partial E}{\partial u} &= \int_{B_\rho} f_x(f_x u + f_y v + f_t) dx dy = 0 \\
0 = \frac{\partial E}{\partial v} &= \int_{B_\rho} f_y(f_x u + f_y v + f_t) dx dy = 0
\end{aligned}
\\
\begin{pmatrix}
\int_{B_\rho} f_x^2 dxdy & \int_{B_\rho} f_x f_y dxdy \\
\int_{B_\rho} f_x f_y dxdy & \int_{B_\rho} f_y^2 dxdy
\end{pmatrix}
\begin{pmatrix}
u \\
v
\end{pmatrix}
=
\begin{pmatrix}
-\int_{B_\rho} f_x f_t dxdy \\
-\int_{B_\rho} f_y f_t dxdy
\end{pmatrix}
Můžeme nahradit integrály za Gaussovské rozmazání, čímž dostaneme "plynulejší okolí"
\begin{pmatrix}
G_{\sigma} * (f_x^2) & G_{\sigma} * (f_x f_y) \\
G_{\sigma} * (f_x f_y) & G_{\sigma} * (f_y^2)
\end{pmatrix}
\begin{pmatrix}
u \\
v
\end{pmatrix}
=
\begin{pmatrix}
-G_{\sigma} * (f_x f_t) \\
-G_{\sigma} * (f_y f_t)
\end{pmatrix}
Snadno vyřešíme Cramerovým pravidlem
Výhody
- Jednoduché, rychlé
- Stačí nám 2 snímky
Nevýhody
- Problémové situace, kde neplatí podmínka konstantnosti - rotace, protijedoucí auta, …
- Nepočítá husté pole toků (jen tam, kde víme gradient)
Horn-Schunck (Globální metoda)
Pouze dva přepoklady:
- Zachování jasu -
f_x u+f_y v + f_t = 0 - Malé změny (Gradient vektorového pole je malý) -
\int_{\Omega} ( \lvert \nabla u \rvert^2 + \lvert \nabla v \rvert^2) dx dyje malé
Kombinací dostáváme funkcionál energie optického toku
E_{HS}(u, v) = \int_{\Omega} ((f_x u + f_y v + f_t)^2 + \alpha (\lvert \nabla u \rvert^2 + \lvert \nabla v \rvert^2)) dx dy
Tento funkcionál minimalizujeme na jediné globální řešení
Výhody
- Jsme schopni řídit smoothness pomocí
\alpha - Produkuje dense flow fields
Nevýhody
- Stále musíme splňovat předpoklad malých změn
- Celkem pomalé a drahé