fi-notes/PGV06_vykreslovani_objemovych_dat.md at f0e56f090f7ac50640aa4b29abe6154f85dfb4e9

Vojtěch Struhár f0e56f090f Revert "Use markdown footnotes"

This reverts commit c35a357e07.
Only the content files

2025-06-07 10:29:28 +02:00

11 KiB

Raw Blame History

title	description
Vykreslování objemových dat	TODO

Note

Rekonstrukce povrchu - kontury, objem, bodový mrak. Algoritmus pochodujících kostek. Přímé vykreslování objemových dat.
PB009, PA010, PA213

Tip

Většina obsahu převzata z původní otázky VPH01 Pokročilá počítačová grafika

Bodový mrak (point cloud)

Množina bodů v prostoru, které nemají žádnou strukturu. Nejjednodušší přístup k renderování objemu, kdy se nepokoušíme o žádnou rekonstrukci povrchu. Body však mohou mít různé barvy a průhlednost.

Při renderování bodových mraků je třeba vyřešit několik souvisejících problémů s daty:

Data s neuniformním vzorkem.
Chybějící data.
Šum a outlieři.

Kromě pozic mohou surová data obsahovat také normály, barvy, apod.

Vykreslování bodových mraků

Ze získaných dat se snažíme vytvořit mesh. Ten lze vyrenderovat tradičním způsobem.

Před samotnou rekonstrukcí je často potřeba provézt ještě předzpracování:

Registration - spojení dat z více pohledů dohromady
Filtering - odstranění šumu a outlierů
Segmentation - rozdělení objektů na jednotlivé části
- Billboarding
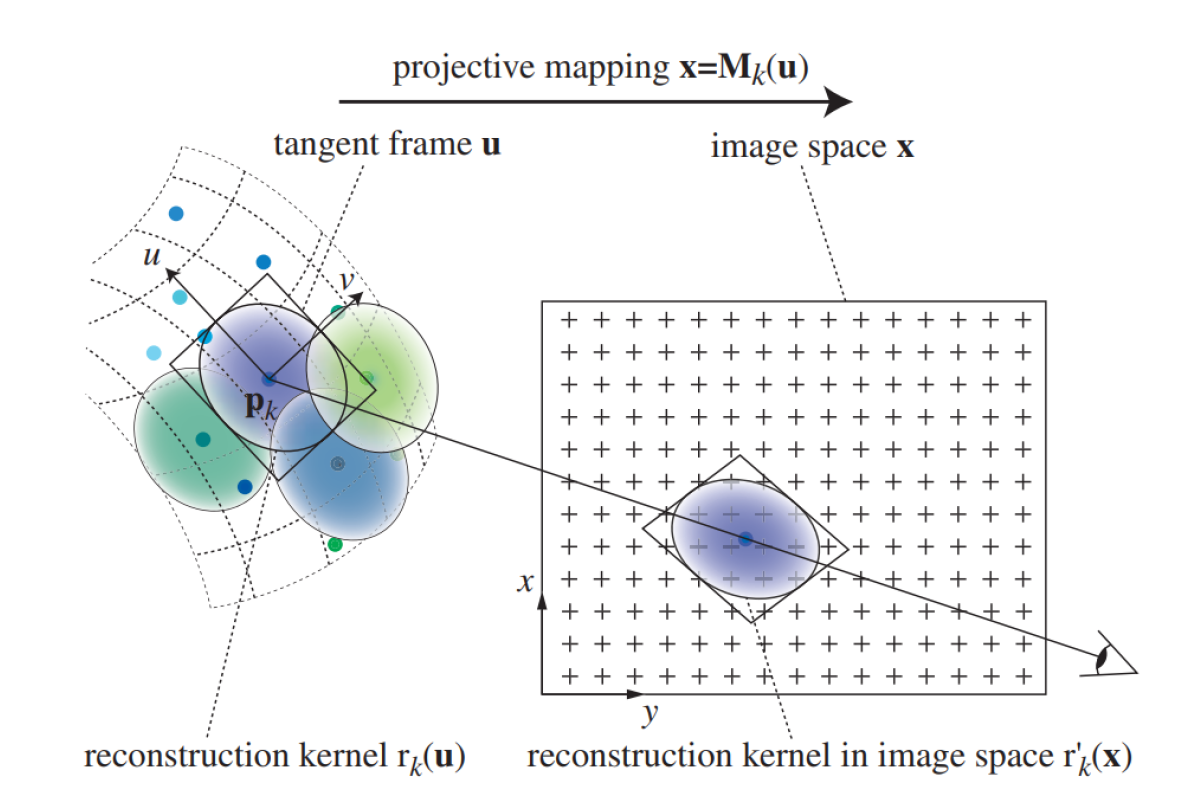
  Vykreslujeme pouze body, nebo obdélníky na místech, kde se body nacházejí. Body mohou být billboardované (otočené ke kameře), nebo využít normálnových dat v bodech (= Splatting).
- Surface Splatting
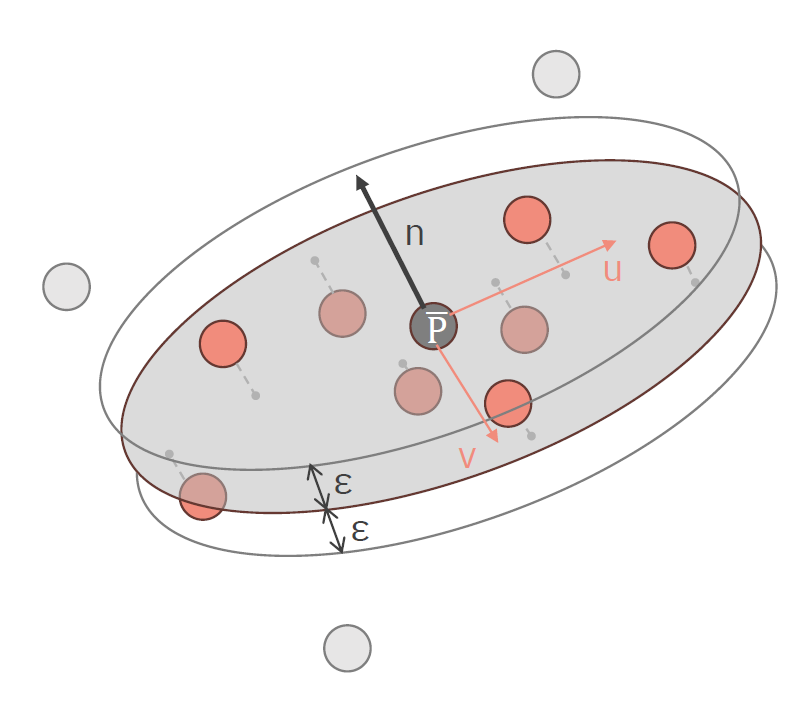
  Normála povrchu odpovídá normále tečné plochy v každém bodě. Pro každý bod najdeme k bodů v okolí, které minimalizuje vzdálenost těchto bodů od naší roviny n = \arg \min*{|n| = 1} \sum*{i=1}^k ((p_i - p) \cdot n)^2 . pa213
  
  Pro nalezení normál využijeme PCA (Principal Component Analysis), normála poté odpovídá vlastnímu vektoru s nejmenší vlastní hodnotou. PCA však vrátí nekonzistentně otočené normály, které můžeme opravit buď otočením všech normál ke kameře, nebo iterativně opravováním sousedství.
  
  Při samotném vykreslování vytvoříme pro každý takový bod elipsu (podle PCA), která bude průhlednější čím dál od středu. S dostatečným množstvím takových elips můžeme vytvořit dojem plochy. Elipsy můžou být stínované podle vypočítané normály, nebo plynule podle normál jednotlivých bodů.

Rekonstrukce povrchu

Delaunay triangulation
Vytváří trojúhelníkovou síť, tak že žádný bod se nenáchází ve vepsané kružnici žádného trojúhelníku. Maximalizuje nejmenší úhel trojúhelníků. delaunay-triangulation

Lze použít ve 3D pro rekonstrukci povrchu, ale je třeba odstranit body, které nejsou součástí povrchu. Zároveň delaunay nedovolí vytvořit díry ve výsledném meshi.
Alpha shapes
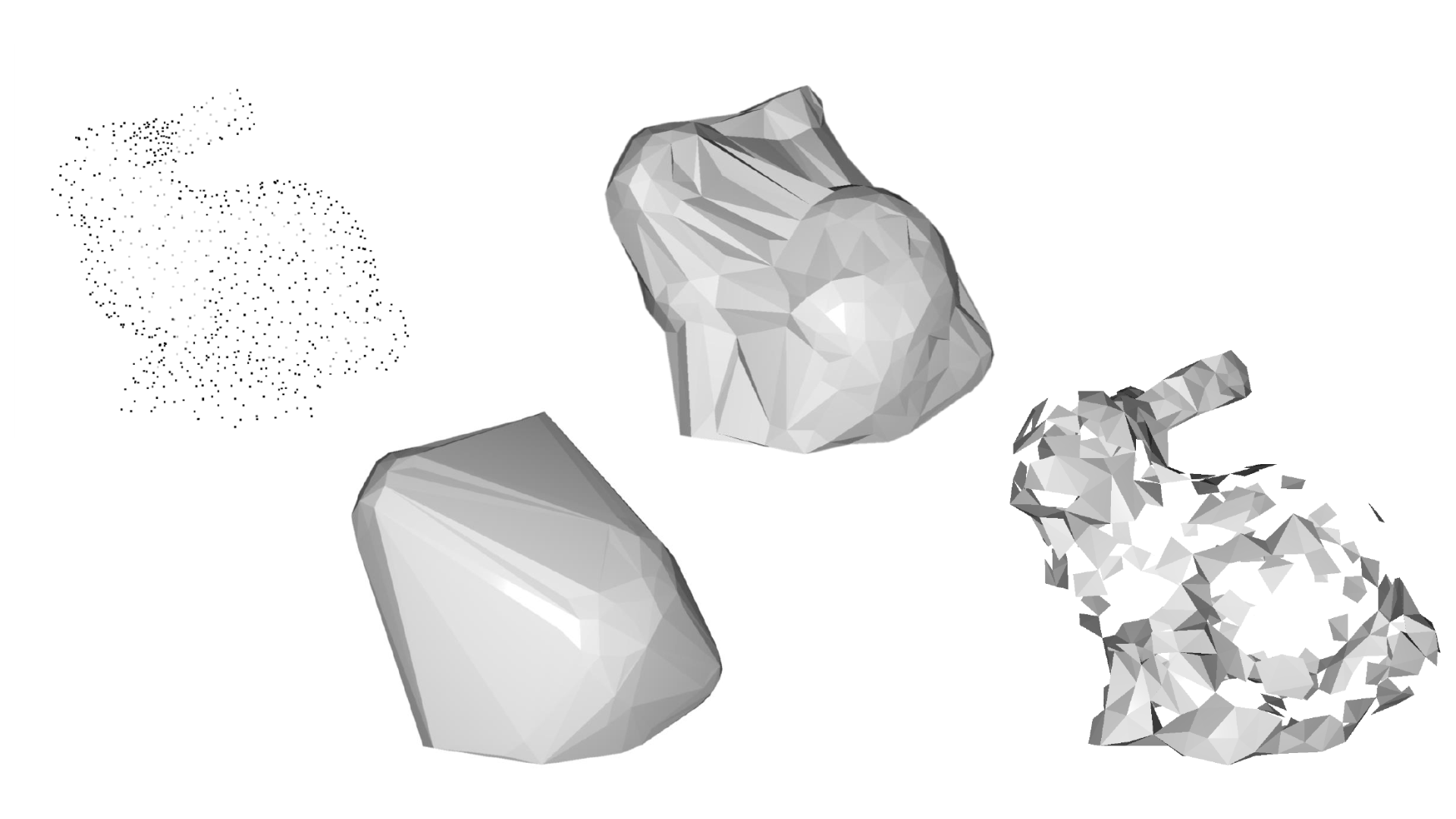
Obecnější metoda než delaunay triangulation, která umožňuje vytvářet i díry ve výsledném meshi. Alpha shapes jsou definovány pomocí parametru alpha, který určuje, jak moc se mohou body "vytahovat" z objemu.

pa213 má hezkou metaforu se zmrzlinou s čokoládovými kousky a sférickou naběračkou. Hodnota parametru alpha určuje, jak velká je naběračka, kterou se snažíme vybírat zmrzlinu tak, abychom se nedotkli čokoládových kousků.

V podstatě zobecnění delaunay triangulation, kde akceptujeme pouze takové trojúhelníky, které mají opsanou kružnici s poloměrem menším než alpha. pa213

Příklady meshe pro různé hodnoty Alpha
Aproximace implicitní funkcí
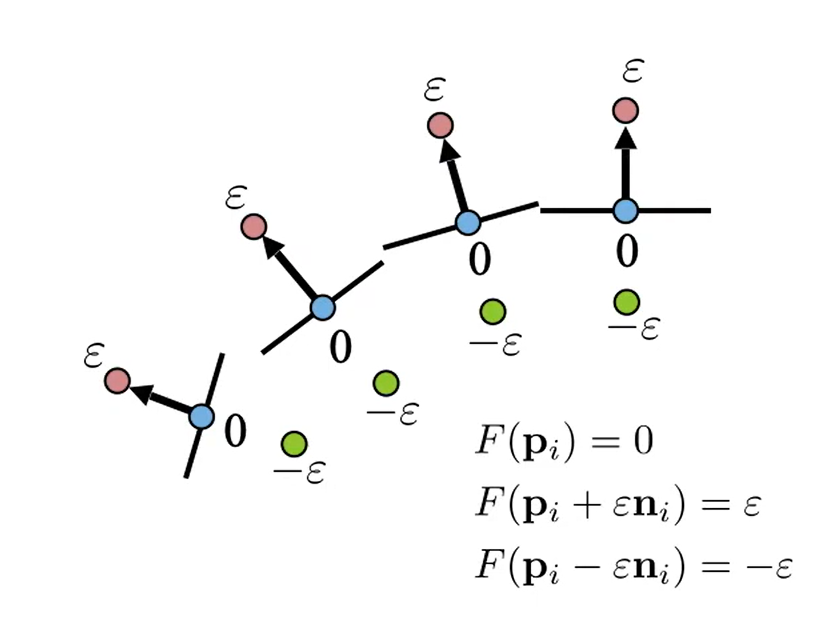
Uvažujme implicitní funkci f(x, y, z), která je signed-distance funkcí od našeho daného povrchu (na povrchu = 0, uvnitř < 0, venku > 0). Taková funkce popisuje povrch jako nulovou hladinu.

Pro definici takové funkce by nám teoreticky stačily body našeho pointcloudu, které všechny nadefinujeme na nulovou hodnotu. Tímto způsobem má však naše funkce trivalní řešení, protože bychom mohli zvolit funkci, která pro všechny body vrací 0. Abochom tomu zabránili, přidáme pro každý bod dva nové body (1 uvnitř a jeden venku) posunuté podél normály. Tímto způsobem získáme funkci, která je nulová na povrchu a má správné znaménko uvnitř a venku.

Objemová data

Voxel
Voxel je 3D analogií pixelu -- bod v prostoru, který má určitou hodnotu (např. barvu, intenzitu, ...). Voxelová data mohou být získána (např. pomocí CT, MRI, PET, atd.) nebo být také výsledkem simulace (např. simulace proudění tekutin).
Objemová data
Objemová data jsou definována nejčastěji jako mřížka voxelů. Mřížky můžou mít různý tvar (pravidelné, nepravidelné, lineární, radiální, ...)

Vykreslování objemových dat

Slicing
Vykreslujeme řezy objemem. Pro každý řez vykreslíme všechny voxely, které řez protíná. Výsledkem je 2D obrazec, který můžeme vykreslit tradičním způsobem. Pro jeden objekt můžeme vytvořit několik řezů a ty pak vykreslit dohromady.

Rekonstrukce povrchu (indirect volume rendering)

Iso-kontury
Na každé vrstvě najdeme kontury 2D obrazců, ty pak mezi vrstvami spojíme. Výsledkem je 3D mesh. Pro nalezení kontur použijeme algoritmy ze zpracování obrazu. Spojení je triviální, pokud provádíme spojení 1:1 (jedna kontura na jedné vrstvě se spojí s jednou konturou na druhé vrstvě). Je třeba speciálně řešit nekonvexní oblasti.

Pokud chceme provést spojení M:N, je třeba vytvořit mezivrstvu, která bude mít 1 konturu vytvořenou ze všech kontur okolních vrstev spojených dohromady. Tím zajistíme korektní aproximaci této situace.
Marching cubes
Uvažme prostor, kde každý voxel obsahuje nějakou hodnotu a my chceme vytvořit povrch pro specifickou hodnotu (typicky 0). Pro tento problém můžeme využít následující algoritmy.

V každém voxelu určí, které jeho rohy jsou uvnitř povrchu a které jsou vně. Takových kombinací existuje 256, ale pouze 16 je unikátních

Marching cubes by Ryoshoru (16. varianta je, pokud všechny body leží uvnitř)

Díky tomu jsme schopní tyto kombinace předpočítat a pro každý voxel vykreslit odpovídající trojúhelníky. Výsledkem je mesh, který reprezentuje povrch objemu. marching-cubes

Je možné tyto předpočítané body interpolovat podél hran, na kterých leží a tím zlepšit výsledný mesh.

Nevýhodou je tzv. Schodišťový efekt, kdy je výsledný mesh velmi hranatý. Zároveň výsledná mesh obsahuje obrovské množství trojúhelníků, což může být neefektivní.
Marching tetrahedra
Analogický k marching cubes, ale používá místo krychlí čtyřstěny. Řeší problém s některými nejednoznačnými konfiguracemi v marching cubes, a taky nikdy nebyl patentován (kdežto marching cubes ano). marching-tetrahedra
Flying edges
Optimalizovaný algoritmus pro marching cubes, který prochází každou hranu pouze jednou.
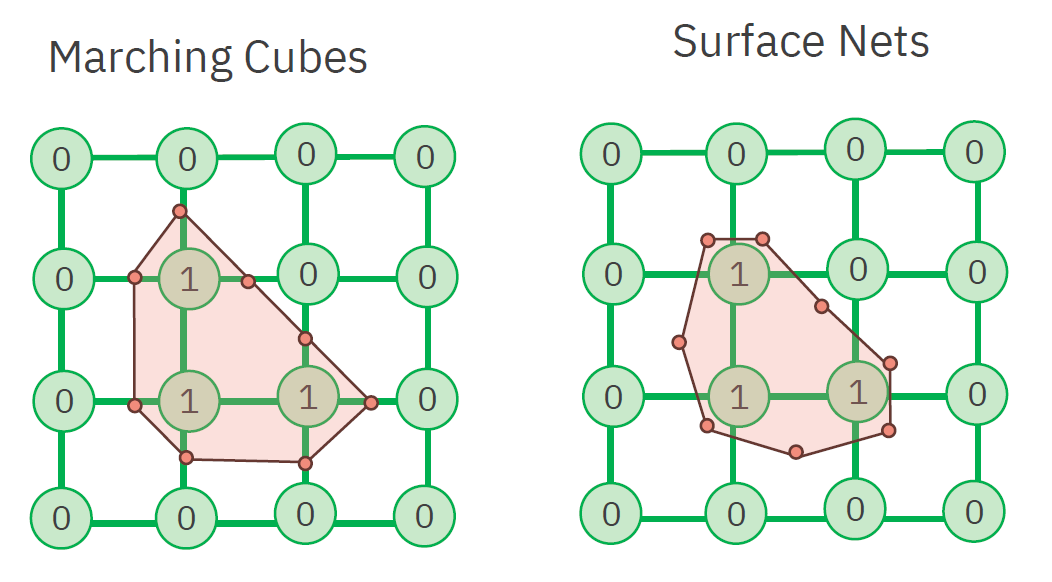
Surface nets
Narozdíl od MC vykresluje vrcholy uvnitř voxelů, čímž odstraňuje problém ostrých hran. Výsledný mesh je tedy mnohem hladší.
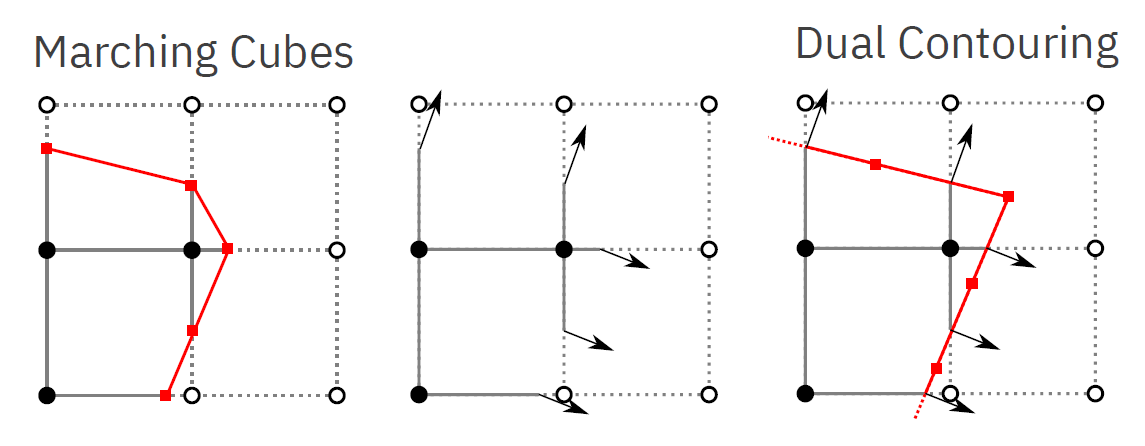
Dual contouring
Z voxelů se stanou vrcholy (tedy využíváme dualního grafu). Tyto vrcholy jsou ale posunuty tak, že povrch může obsahovat jak ostré hrany tak zaoblené plochy. dual-contouring

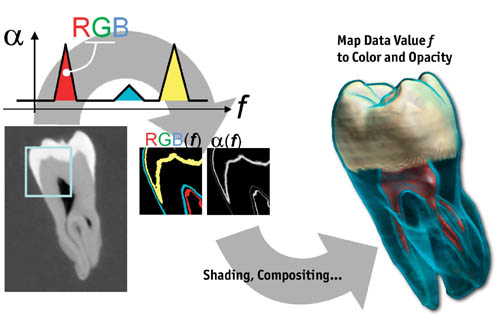
Direct volume rendering (přímé renderování objemu)

Nerekonstruujeme povrch, ale mapujeme data na optické vlastnosti jako je barva a průhlednost. Během renderování se pak využívá path tracing, a tyto vlastnosti se akumulují podél jednotlivých paprsků. gpugems

V realitě tohle chování paprsku popisujeme integrály. V počítačové grafice se ale využívá aproximace pomocí sumy.

The Process of Volume Rendering gpugems

Emmission-absorption model
Paprsek vstupuje do objemu, kde je absorbován a emitován. Výsledná barva je pak výsledkem akumulace těchto vlastností. V notaci používáme: pa213
- \kappa je funkce absorpce,
- q je emise.
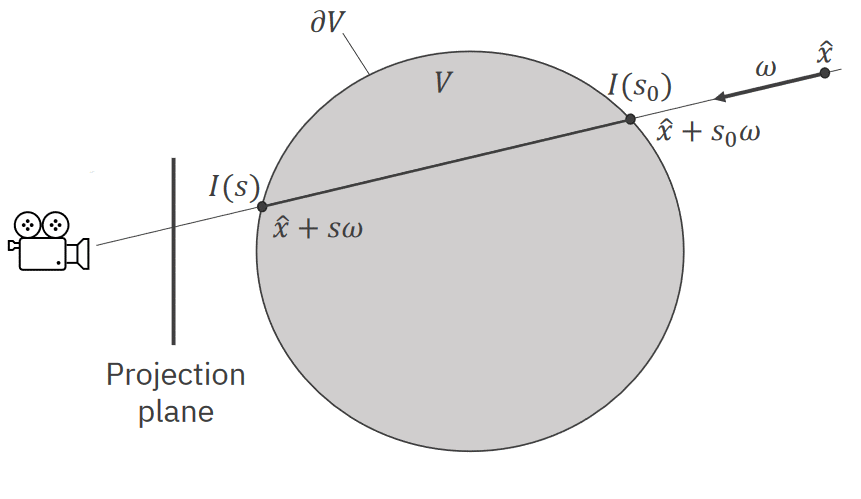
Optická hloubka / optical depth
Bezrozměrná veličina \tau, která popisuje, jak moc jde "vidět skrz" něco, třeba plyn. Čím větší, tím méně vidíme.

Z jiné perspektivy je to akumulovaná absorpce na paprsku. Optická hloubka mezi dvěma body s_1 a s_2 na paprsku je dána jako:
```
\tau(s_1, s_2) = \int_{s_1}^{s_2} \kappa(s) ds
```
Průhlednost / transparency
Průhlednost popisuje, jak dobře vidíme skrz objem. Upadá exponenciálně s růstem optické hloubky.

Průhlednost mezi dvěma body s_1 a s_2 na paprsku je dána jako:
```
\theta(s_1, s_2) = e^{-\tau(s_1, s_2)}
```
Volume rendering integral
Intenzitu světla I v místě paprsku s počítáme pomocí: pa213
```
\begin{aligned}

I(s) &= I(s_0) \cdot \theta(s_0, s) + \int_{s_0}^s q(s') \cdot \theta(s', s) ds' \\

&= I(s_0) \cdot e^{-\tau(s_0, s)} + \int_{s_0}^s q(s') \cdot e^{-\tau(s', s)} ds'

\end{aligned}
```
kde:
- s_0 je místo, kde se paprsek dostal dovnitř nějakého světlo-vyzařujícího objemu,
- I(s_0) je boundary light, tedy světlo na hranici objemu,
- q(s') je emise v bodě s'.
Back-to-front
Přístup k počítání I, kdy paprsky vyhodnocujeme od hranice objemu dále od kamery směrem ke kaměře.

Výhoda je, že nemusíme udržovat proměnnou pro průhlednost. Nevyhoda je, že musíme vyhodnotit všechny voxely v cestě paprsku, protože "přepisují" výsledek.
Front-to-back
Přístup k počítání I, kdy paprsky vyhodnocujeme od hranice objemu blíže ke kameře směrem od kamery.

Dá se utnout dřív, když víme jistě, že už je výsledek neprůhledný a tedy už se nic nezmění.
Transfer function
Funkce T, která mapuje hodnoty voxelů na barvu a průhlednost. Klasifikuje voxely. pa213

Zdroje

[pa010-2020,1] Sochor: PA010 Intermediate Computer Graphics (podzim 2020)
[pa213, 2] PA213 Advanced Computer Graphics
[marching-cubes,3] Marching cubes: A high resolution 3D surface construction algorithm
[marching-tetrahedra,4] Wikipedia: Marching tetrahedra
[dual-contouring,5] Dual Contouring Tutorial
[delaunay-triangulation,6] Wikipedia: Delaunay triangulation
[gpugems,7] GPU Gems: Volume Rendering Techniques

11 KiB Raw Blame History