20 KiB
| title | description |
|---|---|
| Strojové učení | TODO |
Note
Strojové učení a rozpoznávání vzorů: problém klasifikace a regrese, shluková analýza, učení s učitelem a bez učitele. Vícevrstvé neuronové sítě, vícevrstvé perceptrony, ztrátové funkce, zpětná propagace. ~Hopfieldova síť,~ konvoluční sítě, rekurentní sítě ~, samo-organizující mapy~ .
PV021
Tip
Velkou část zpracování téhle otázky jsem ukradl sám sobě.
Strojové učení a rozpoznávání vzorů
-
Machine learning / strojové učení
Oblast informatiky zabývající se konstrukcí systémů, které nemají svoji funkcionalitu explicitně naprogramovanou, ale naučí se ji až na základě vstupních dat. 1 2
Používá se např. pro:
- filtrování spamu v emailech,
- rozpoznávání řeči, rukopisu, tváří, zvuků, atd.,
- klasifikaci textů,
- herní strategie,
- analýzu trhu,
- autonomní řízení vozidel.
-
Rozpoznávání vzorů / pattern recognition
Problém automatizovaného rozpoznávání vzorů v datech (např. číslic v obrázku). Příklady jsou klasifikace, regrese a shluková analýza. 3 -
Klasifikace
Problém identifikace kategorie, do které patří vstupní data. Výstupem klasifikace je buď jedna konkrétní kategorie nebo vektor popisující s jakou pravděpodobností vstup do každé kategorie patří. 4 -
Regrese
Problém odhadu hodnoty nějaké proměnné na základě znalosti jiných proměnných. Výstupem regrese je obvykle reálné číslo. 5Například při lineární regresi se snažíme data napasovat na přímku -- najít její offset a směrnici. Při logistické regresi chceme to samé ale místo přímky máme logistic sigmoid. A tak dále. 2
-
Shluková analýza / cluster analysis
Vicedimenzionální problém rozdělení vstupních dat do skupin (shluků) tak, aby data v jednom shluku byla podobnější sobě než datům v jiných shlucích. 6Souvisejícím problémem je vyjádření toho, že jsou si data v nějakém smyslu podobná.
-
Supervised learning / učení s učitelem
Síť se učí na základě množiny trénovacích vstupů ve formátu (vstup, výstup). Supervised learning algoritmy se snaží síť modifikovat tak, aby vracela výstupy co možná nejpodobnější těm trénovacím. 2 -
Unsupervised learning / učení bez učitele
Síť dostává jen vstupy. Cílem je získat o vstupní množině dat nějakou užitečnou informaci, třeba kde jsou shluky. 2
Neuronové sítě
-
Neural network / neuronová síť
Neuronová síť je množina propojených neuronů, jejíž chování je zakódováno do spojení mezi neurony. Je primitivním modelem biologických neuronových sítí.
Typ neuronové sítě je dán její architekturou (způsobem zapojení), aktivitou (transformací vstupů na výstupy) a učením (metodou změny vah při trénování).
-
Architektura
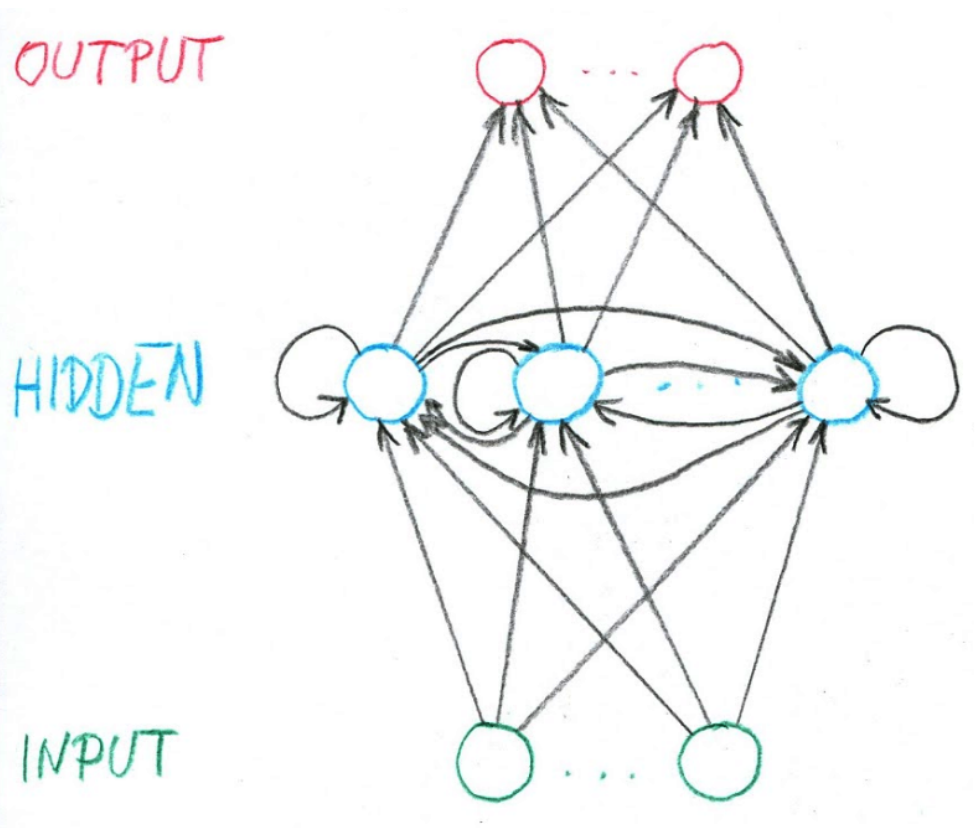
Neuron může být input, output nebo hidden. Může být dokonce input i output najednou. Hidden je, právě když není input ani output.Síť být cyklická -- recurrent -- nebo acyklická -- feed-forward.
-
Stav sítě
Vektor výstupů všech neuronů sítě (nejen output). -
Stavový prostor sítě
Množina všech možných stavů sítě. -
Vstup sítě
Vektor reálných čísel (prvek\Reals^n), kdenje počet vstupů. -
Vstupní prostor sítě
Množina všech vstupů sítě. -
Iniciální stav
Input neuronům je za výstup (y) dán vektor vstupů (\vec{x}). Všem ostatním neuronům je výstup (y) nastaven na 0. -
Výstup sítě
Vektor výstupů (y) output neuronů. Výstup se v průběhu výpočtu může měnit. -
Výpočet
Typicky po diskrétních krocích:-
Zvolí se množina neuronů (vybrané podle pravidla daného architekturou).
-
Zvoleným neuronům je nastaven výstup -- prostě se vyhodnotí aktivační funkce.
-
Vrať se ke kroku 1.
Výpočet je konečný, pokud se stav sítě dále nemění po konečném množství opakování postupu výše.
-
-
Konfigurace
Vektor hodnot všech vah. -
Vahový prostor
Množina všech konfigurací. -
Iniciální konfigurace
Počáteční hodnoty vah (než začne trénování).
Multilayer perceptron (MLP) / vícevrstvé neuronové sítě
-
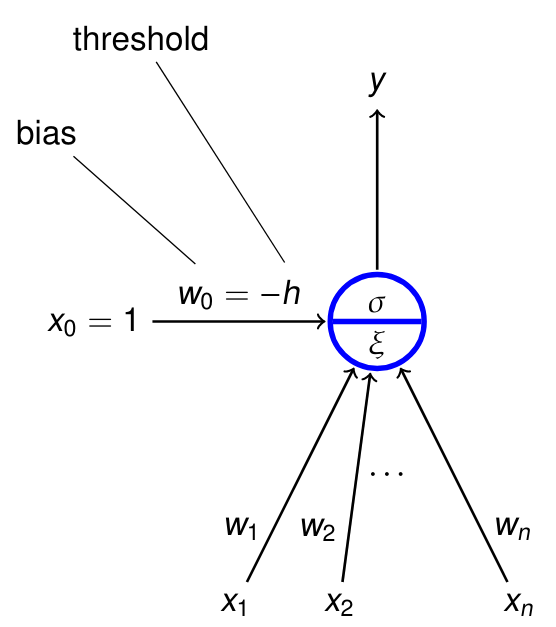
Perceptron -- jeden neuron
- Hrubá matematická aproximace biologického neuronu.
- Binární klasifikátor -- rozlišuje jestli vstup patří nebo nepatří do nějaké jedné kategorie.2
- Linerání klasifikátor -- jeho funkce kombinuje vstupy lineárně.
x_i-- inputyw_i-- váhy\xi = w_0 + \sum_{i=1}^n w_i x_i-- vnitřní potenciály-- výstupy = \sigma(\xi)-- aktivační funkce udávající výstup- bias -- udává "jak těžké" je pro neuron se aktivovat (čím vyšší číslo, tím těžší je pro neuron vydat nenulový výstup)
x_0-- pro snažší implementaci se závádí dodatečný vstup, který má vždy hodnotu 1 a váhu rovnu -bias
Note
Vnitřní potenciál funguje jako nadrovina (čára při 2D, rovina při 3D, nepředstavitelný mostrum ve vyšších dimenzí), která rozděluje prostor vstupů na část, kde je
\xi < 0a kde\xi > 0. -
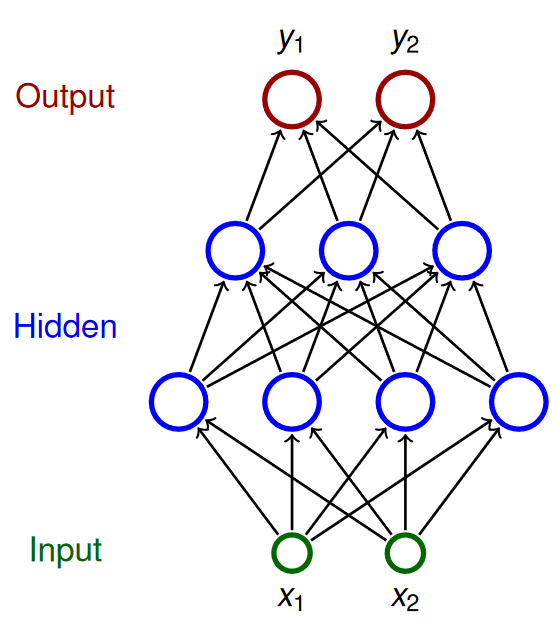
Multilayer perceptron (MLP)
MLP je feed-forward (neobsahuje cykly) architektura NN, kde platí:
- Neurony rozděleny do vrstev -- jedné vstupní, jedné výstupní a libovolného počtu skrytých vrstev uprostřed.
- Vrstvy jsou dense -- každý neuron v $i$-té vrstvě je napojen na každý neuron v $(i + 1)$-ní vrstvě.
Kde:
\textcolor{green}{X}-- množina input neuronů\textcolor{red}{Y}-- množina output neuronůZ-- množina všech neuronů- Neurony mají indexy
i,j, ... \xi_j-- vnitřní potenciál neuronujpo skončení výpočtuy_j-- výstup neuronujpo skončení výpočtux_0 = 1-- hodnota formálního jednotkového vstupu (kvůli biasům)w_{j,i}-- váha spojení z neuronuido neuronuj(dst <- src)w_{j,0} = -b_j-- bias -- váha z formální jednotky do neuronujj_{\leftarrow}-- množina neuronůi, jenž mají spojení doj(j <- i)j^{\rightarrow}-- množina neuronůi, do nichž vede spojení zj(j -> i)
Aktivita
-
Pravidlo pro výběr neuronů při výpočtu
V i-tému kroku vezmi i-tou vrstvu. -
Vnitřní potenciál neuronu $j$
\xi_j = \sum_{i \in j_{\leftarrow}} w_{ji}y_i -
Aktivační funkce neuronu $j$
\sigma_j : \Reals \to \Reals(třeba logistic sigmoid) -
Stav nevstupního neuronu $j$
y_j = \sigma_j(\xi_j)resp.y_j(\vec{w}, \vec{x}) -
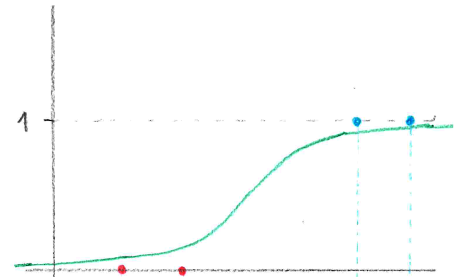
Logistic sigmoid
Většina aktivačních funkcí vychází s funkce sigmoid. (Jsou sigmoidní, vypadají trochu jako písmenoS). Přidávají do výpočtu nelinearitu, která je potřeba, aby NN mohla modelovat libovolné funkce. Zároveň je podobná klasickému thresholdu, ale je "vyhlazená".\sigma(\xi) = \frac{1}{1 + e^{-\lambda \cdot \xi}}kde
\lambdaje steepness parametr, který určuje, jak rychle sigmoid roste.
Trénink
Important
Pro likelihood viz otázka Statistika.
Neuronka je model, kde váhy neuronů jsou parametry. Při učení neuronek je naším cílem maximalizovat likelihood, jakožto míru toho, že naše síť sedí na "naměřená data", training set \cal T. Tomuhle přístupu se říká maximum likelihood principle.
-
Training set $\cal T$
je množinapsamplů, kde\vec{x} \in \Reals^{|X|}jsou vstupní vektory a\vec{d} \in \Reals^{|Y|}jejich očekáváné výstupy.\mathcal{T} = \{(\vec{x}_1, \vec{d}_1), (\vec{x}_2, \vec{d}_2), ..., (\vec{x}_p, \vec{d}_p)\} -
Ztrátové funkce / loss function / error function
Popisuje způsob, jakým je při tréninku výstup z NN porovnán s očekáváným výstupem.Její volba závisí na tom, co NN modeluje. Např. volíme:
-
mean squared error (MSE) -- pro regresi,
\begin{aligned} E_k(\vec{w}) &= \frac{1}{2} \sum_{j \in Y} \left( y_j(\vec{w}, \vec{x_k}) - d_{kj} \right)^2 \\ E(\vec{w}) &= \textcolor{red}{\frac{1}{p}} \sum_{k=1}^p E_k(\vec{w}) \end{aligned} -
(categorical) cross-entropy -- pro (multi-class) klasifikaci.
\begin{aligned} E(\vec{w}) = -\frac{1}{p} \sum_{k=1}^p \sum_{j \in Y} d_{kj} \ln(y_j) \end{aligned}
-
-
Gradient descent
Algoritmus počítající, jak se mají vahy neuronů upravit, aby se zmenšila ztráta. Vychází z gradientu ztrátové funkce.\Delta \vec{w}^{(t)} = - \varepsilon(t) \cdot \nabla E (\vec{w}^{(t)}) -
Stochastic Gradient Descent (SGD)
Sample nebereš po jednom ale po malých randomizovaných várkách -- minibatchíchT, a váhy upravuješ až po zpracování minibatche.\Delta \vec{w}^{(t)} = - \varepsilon(t) \cdot \sum_{k \in T} \nabla E_k(\vec{w}^{(t)}) -
Backpropagation / zpětná propagace
Technika, kdy se v průběhu gradient descent ztráta způsobená konkrétním neuronem dedukuje na zákládě jeho příspěvku k výsledku. Algoritmus tak postupuje od output vrstvy směrem k input vrstvě. -
Learning rate $\varepsilon$
Hyperparametr0 < \varepsilon \le 1ovlivňující rychlost učení. Může záviset na iteracit, pak je to funkce\varepsilon(t).
Gradient descent v MLP
\begin{aligned}
w_{ji}^{(t+1)}
&= w_{ji}^{(t)} + \Delta w_{ji}^{(t)} \\
\Delta w_{ji}^{(t)}
&= -\varepsilon(t) \cdot \textcolor{green}{\frac{\partial E}{\partial w_{ji}}(\vec{w}^{(t)})} \\
\textcolor{green}{\frac{\partial E}{\partial w_{ji}}}
&= \sum_{k=1}^{p} \textcolor{blue}{\frac{\partial E_k}{\partial w_{ji}}} \\
\textcolor{blue}{\frac{\partial E_k}{\partial w_{ji}}}
&= \textcolor{red}{\frac{\partial E_k}{\partial y_j}}
\cdot \textcolor{purple}{\frac{\partial y_j}{\partial \xi_j}}
\cdot \textcolor{teal}{\frac{\partial \xi_j}{\partial w_{ji}}} \\
&= \textcolor{red}{\frac{\partial E_k}{\partial y_j}}
\cdot \textcolor{purple}{\sigma'_j(\xi_j)}
\cdot \textcolor{teal}{y_i}
\end{aligned}
Za předpokladu, že E je squared error, pak:
Warning
V případě, že
Enení squared error, následující výpočet neplatí.
\large
\textcolor{red}{\frac{\partial E_k}{\partial y_j}} =
\begin{cases}
y_j - d_{kj} & \text{ pokud } j \in Y ; \\
\sum_{r \in j^{\rightarrow}} \textcolor{brown}{\frac{\partial E_k}{\partial y_r}}
\cdot \textcolor{dodgerblue}{\frac{\partial y_r}{\partial \xi_r}}
\cdot \textcolor{forestgreen}{\frac{\partial \xi_r}{\partial y_j}}
= \sum_{r \in j^{\rightarrow}} \textcolor{brown}{\frac{\partial E_k}{\partial y_r}}
\cdot \textcolor{dodgerblue}{\sigma'_r(\xi_r)}
\cdot \textcolor{forestgreen}{w_{rj}}
& \text{ jinak}.
\end{cases}
Algoritmus pro výpočet $\frac{\partial E}{\partial w_{ji}}$
- Inicializuj
\varepsilon_{ji} := 0. - forward pass -- vyhodnoť NN pro sample
k(t.j.y_j(\vec{w}, \vec{x_k})pro všechnyj \in Z) - backward pass -- od konce pro každou vrstvu spočítej $\frac{\partial E_k}{\partial y_j}$
a. pokud
j \in Y, pak $\frac{\partial E_k}{\partial y_j} = y_j - d_{kj}$ b. pokudj \in Z \setminus Y \cup X, ajje v $l$-té vrstvě, pak\frac{\partial E_k}{\partial y_j} = \sum_{r \in j^{\rightarrow}} \frac{\partial E_k}{\partial y_r} \cdot \sigma'_r(\xi_r) \cdot w_{rj} - weight update -- pro všechna
w_{ji}spočítej\frac{\partial E_k}{\partial w_{ji}} := \frac{\partial E_k}{\partial y_j} \cdot \sigma'_j(\xi_j) \cdot y_i \varepsilon_{ji} := \varepsilon_{ji} + \frac{\partial E_k}{\partial w_{ji}}\varepsilon_{ji}obsahuje výslednou hodnotu\frac{\partial E}{\partial w_{ji}}
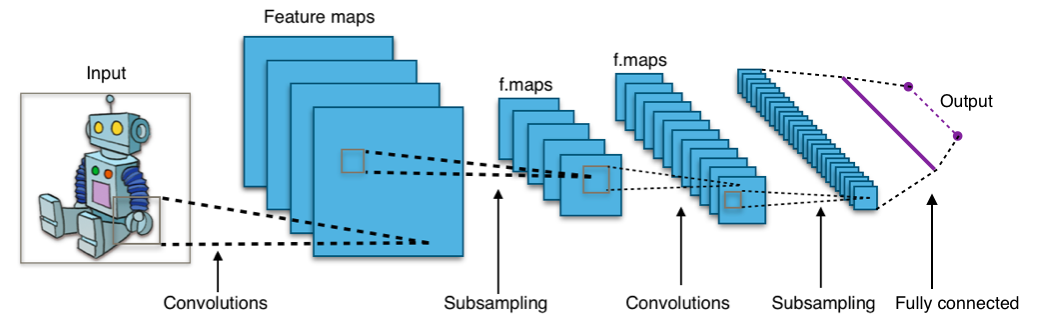
Konvoluční sítě
Neuronové sítě uzpůsobené ke zpracování obrazu. Místo násobení matic používají alespoň v jedné vrstvě konvoluci. Konvoluční sítě mají dva nové typy vrstev: konvoluční a pooling, ale jinak se od klasických MLP moc neliší. Aktivace a trénink zůstavají v podstatě stejné. 7
Important
Pro konvoluci viz otázka Zpracování rastrového obrazu.
Typical CNN by Aphex34
-
Konvoluční vrstva
- Každý neuron je napojen jen na malý receptive field neuronů o vrstvu níže, který se posouvá o daný stride.
- Výstup z neuronu v konvoluční vrstvě je dán konvolucí jeho receptive field s váhami a přičtením biasu.
- Všechny neurony v konvoluční vrstvě sdílí stejné váhy a biasy dané velikostí receptive field, což jim umožňuje naučit se nějaký vzor o velikosti receptive field -- říkáme, že taková vrstva je feature mapa.
- Vzorů se chceme zpravidla naučit více, máme vícero vzájemně nezávislých feature map napojených na stejnou vstupní vrstvu.
-
Pooling vrstva
Nemají váhy. Slouží ke snížení počtu parametrů. Každý neuron počítá nějakou jednoduchou funkci na svém receptive field:- max-pooling: maximum,
- L2-pooling: square root of sum of squares,
- average-pooling: mean.
-
Backpropagation
Algoritmus je potřeba trochu poupravit, aby podporovat konvoluční a pooling vrstvy.
U konvolučních vrstev nestačí pro každou váhu
w_{ji}spočítat\frac{\partial E_k}{\partial w_{ji}}, protože pro každou váhu existuje víc než jeden výstupy_j. Tedy:\frac{\partial E_k}{\partial w_{ji}} = \sum_{rl \in \textcolor{red}{\bf \lbrack ji \rbrack}} \frac{\partial E_k}{\partial y_r} \cdot \sigma'_r(\xi_r) \cdot y_lkde
\color{red}\bf \lbrack ji \rbrackje množina spojení (dvojic neuronů) sdílících váhuw_{ji}.Pokud
j \in Z \setminus Yaj^{\rightarrow}je max-pooling, pakj^{\rightarrow} = \{ i \}a platí:\frac{\partial E_k}{\partial y_j} = \begin{cases} \frac{\partial E_k}{\partial y_i} & \text{pokud } j = \argmax_{r \in i_{\leftarrow}} y_r \\ 0 & \text{jinak} \end{cases}
Rekurentní sítě
Neuronové sítě, jejichž architektura obsahuje cykly. Tedy výstup v jednom bodě v čase sítě přispívá k výstup v budoucnosti. Jinými slovy, je to neuronka s pamětí. Recurrent neural networks (RNN) konkrétně jsou MLP minimálně rozšířené tak, aby měly paměť. 8
-
Výhody
- Umí zpracovat vstupy s variabilní, předem neznámou délkou.
- Velikost modelu (množiny vah) je fixní nezávisle na velikosti vstupu.
- Váhy se sdílí mezi vstupy (např. slova ve větě), což umožňuje naučit se nějaký kontext.
-
Nevýhody
- Trénování je složitější, protože se vyskytuje zpětná vazba.
- Výpočetně náročnější.
- Gradient může explodovat (exploding) nebo zaniknout (diminishing).
-
Notace
V časet:\vec{x_t} = (x_{t, 1}, x_{t, 2}, ..., x_{t, M})je vstupní vektor předávanýMvstupním neuronům,\vec{h_t} = (h_{t, 1}, h_{t, 2}, ..., h_{t, H})je vektor hodnotHskrytých neuronů,\vec{y_t} = (y_{t, 1}, y_{t, 2}, ..., y_{y, N})je výstupní vektorNneuronů,U_{j, i}je váha mezi inputemia hiddenemj,W_{j', i'}je váha mezi hiddenemi'a hiddenemj',V_{j'', i''}je váha mezi hiddenemi''a outputemj''.
-
Aktivita
-
Na počátku je výstup neuronky vynulován. Paměť je tedy prázdná.
-
RNN zpracovává sekvenci vstupů
\mathbb{x} = \vec{x_1}, \vec{x_2}, ..., \vec{x_T}délkyT. -
Pro každý prvek
\vec{x_t} \in \mathbb{x}, síť vyprodukuje výstup z hidden neuronů:\vec{h_t} = \sigma(U \cdot \vec{x}_t + W \cdot \vec{h}_{t-1}) -
Pro výstup pak:
\vec{y_t} = \sigma(V \cdot \vec{h}_t)
-
-
Trénink
Trénovací set je množina dvojic -- (vstupní sekvence, výstupní sekvence).
\mathcal{T} = \{ (\bold{x}_1, \bold{d}_1), ..., (\bold{x}_p, \bold{d}_p) \}Note
Ano, to znamená, že
x_{lt1}je první prvek $t$-ho prvku v $l$-té vstupní sekvenci.Squared error samplu
(\bold{x}, \bold{d}):E_{(\bold{x}, \bold{d})} = \sum_{t=1}^T \sum_{k=1}^N \frac{1}{2} (y_{tk} - d_{tk})^2Gradient descent je podobný. Na začátku jsou všechny váhy inicalizovány poblíž 0 a pak iterativně přepočítávány:
\begin{aligned} U_{kk'}^{(l+1)} &= U_{kk'}^{(l)} - \varepsilon(l) \cdot \frac{\partial E_{(x, d)}}{\partial U_{kk'}} \\ V_{kk'}^{(l+1)} &= V_{kk'}^{(l)} - \varepsilon(l) \cdot \frac{\partial E_{(x, d)}}{\partial V_{kk'}} \\ W_{kk'}^{(l+1)} &= W_{kk'}^{(l)} - \varepsilon(l) \cdot \frac{\partial E_{(x, d)}}{\partial W_{kk'}} \\ \frac{\partial E_{(x, d)}}{\partial U_{kk'}} &= \sum_{t=1}^T \textcolor{brown}{\frac{\partial E_{(x, d)}}{\partial h_{tk}}} \cdot \sigma' \cdot x_{tk'} \\ \frac{\partial E_{(x, d)}}{\partial V_{kk'}} &= \sum_{t=1}^T \textcolor{darkgreen}{\frac{\partial E_{(x, d)}}{\partial y_{tk}}} \cdot \sigma' \cdot h_{tk'} \\ \frac{\partial E_{(x, d)}}{\partial W_{kk'}} &= \sum_{t=1}^T \textcolor{brown}{\frac{\partial E_{(x, d)}}{\partial h_{tk}}} \cdot \sigma' \cdot h_{(t-1)k'} \\ \end{aligned}Za předpokladu squared error je backpropagation:
\begin{aligned} \textcolor{darkgreen}{\frac{\partial E_{(x, d)}}{\partial y_{tk}}} &= y_{tk} - d_{tk} \\ \textcolor{brown}{\frac{\partial E_{(x, d)}}{\partial h_{tk}}} &= \sum_{k'=1}^N \textcolor{darkgreen}{\frac{\partial E_{(x, d)}}{\partial y_{tk'}}} \cdot \sigma' \cdot V_{k'k} + \sum_{k'=1}^H \textcolor{brown}{\frac{\partial E_{(x, d)}}{\partial h_{(t+1)k'}}} \cdot \textcolor{red}{\sigma' \cdot W_{k'k}} \end{aligned}Tip
Pokud
\textcolor{red}{\sigma' \cdot W_{k'k}} \not\approx 1, pak gradient buď vybouchne nebo se ztratí.