17 KiB
| title | description |
|---|---|
| Modelování a projekce | A guide in my new Starlight docs site. |
Note
Homogenní souřadnice, modelovací, pohledová a projekční matice, perspektivní a ortografická projekce. Základní afinní transformace.
PV189, PV112
Souřadnicové systémy
-
Right-hand rule Mnemotechnická pomůcka pro určení orientace os v kartézské soustavě souřadnic. Taky se používá pro určení směru vektorového součinu.
Tip
Osa X je dána ukazováčkem, osa Y prostředníčkem, osa Z palcem. Pokud Y míří nahoru, pak ano, člověk si u toho může vykroutit ruku, ale alespoň si to zapamatuje.
-
Kartézská soustava souřadnic Right-handed systém definován třemi kolmými osami. Ve 2D jsou to
xay. Ve 3D jsou tox,yaz. Jsou na sebe v zájemně kolmé. Počátek je v bodě, kde se protínají všechny osy, označovaném jako0. -
Homogenní souřadnice Hack, kdy reprezentujeme souřadnici v 3D prostoru pomocí 4 čísel, abychom mohli zapsat translaci pomocí matice. Využívá se v projektivní geometrii, pro projekci 3D scén na 2D plochu.
Převod z kartézských na homogenní souřadnice:
(x, y, z) \to (x, y, z, 1).Převod z homogenních na kartézské souřadnice:
(x, y, z, w) \to (\frac{x}{w}, \frac{y}{w}, \frac{z}{w}).Body, kde
w = 0jsou body v nekonečnu. Využívá se pro popis pohybu k nekonečnu, který se v kartézských souřadnicích nedá popsat.
MVP matice
Important
Pro implementaci v OpenGL viz Renderování s využitím GPU.
Warning
Při zápisu matic bacha na to, jestli jsou row-major nebo column-major. Třeba v OpenGL to znamená, že se všechny matice píší v transponované podobě, jelikož OpenGL je column-major a v takovém pořádí jsou i parametery
mat2,mat3amat4V GLSL.
-
Modelovací matice $M$ Převádí souřadnice z prostoru objektu (local space) do prostoru světa (world space). Využívá se pro rotaci (
R), škálování (S) a translaci (T) objektu.M = T \cdot R \cdot S -
Pohledová matice / view matrix $V$
Převádí souřadnice z prostoru světa (world space) do prostoru před kamerou (camera space). Otáčí světem, aby kamera byla jeho středem.1V = \begin{bmatrix} \color{red}{R_x} & \color{red}{R_y} & \color{red}{R_z} & 0 \\ \color{green}{U_x} & \color{green}{U_y} & \color{green}{U_z} & 0 \\ \color{blue}{D_x} & \color{blue}{D_y} & \color{blue}{D_z} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & -\color{purple}{P_x} \\ 0 & 1 & 0 & -\color{purple}{P_y} \\ 0 & 0 & 1 & -\color{purple}{P_z} \\ 0 & 0 & 0 & 1 \end{bmatrix}kde:
-
\color{red}{R}je vektor, který ukazuje doprava od kamery. -
\color{green}{U}je vektor, který ukazuje nahoru od kamery. -
\color{blue}{D}je vektor, který ukazuje dopředu od kamery. -
\color{purple}{P}je pozice kamery.Note
Všimni si, že levá matice je transponovaná a poziční vektor v pravé matici je negovaný. Je to proto, že otáčíme a posouváme celým světem tak, aby kamera byla v počátku, musíme proto provést inverzní operace vůči těm, které chceme provést s kamerou. 1
-
-
Frustum Část 3D tělesa (nejčastěji pyramidy nebo jehlanu) mezi dvěma rovnoběžnými rovinami. Doslovný překlad je "komolý jehlan"
-
Projekční matice / projection matrix $P$ Převádí souřadnice z prostoru před kamerou (camera space) do clip space.
Používá se zejména ortografická projekce (
P_\text{ortho}) a perspektivní projekce (P_\text{persp}). -
MVP matice Pro převod modelu z jeho lokálního prostoru do clip space použijeme:
\vec{v}_\text{clip} = P \cdot V \cdot M \cdot \vec{v}_\text{local}
Projekce
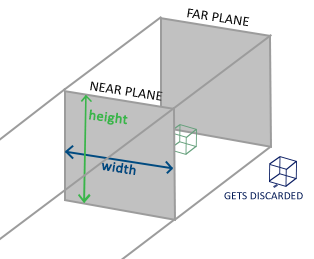
Ortografická projekce
Používáme především k vykreslení 2D scén. Osu Z můžeme využít, abychom jeden sprite schovali za jiný. Nicméně objekty dál od kamery jsou stejně velké jako ty blízko kamery. 1
Je dána 6 parametry:
\text{left}- levá hranice (X),\text{right}- pravá hranice (X),\text{bottom}- spodní hranice (Y),\text{top}- horní hranice (Y),\text{near}- blízká hranice (Z),\text{far}- daleká hranice (Z).
Společně definují boxík, kde je (\text{left}, \text{bottom}, -\text{near}) levý spodní roh a (\text{right}, \text{top}, -\text{far}) pravý horní roh. Úkolem matice P_\text{ortho} je nasoukat tento boxík do krychle (-1, -1, -1) \to (1, 1, 1) (a navíc flipnou Z, protože OpenGL mění handedness).
\begin{aligned}
P_\text{ortho} &= C \cdot S \cdot T \\
&=
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\cdot
\begin{bmatrix}
\frac{2}{\text{right-left}} & 0 & 0 & 0 \\
0 & \frac{2}{\text{top-bottom}} & 0 & 0 \\
0 & 0 & \frac{2}{\text{far-near}} & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\cdot
\begin{bmatrix}
1 & 0 & 0 & -\frac{\text{right+left}}{2} \\
0 & 1 & 0 & -\frac{\text{top+bottom}}{2} \\
0 & 0 & 1 & -\frac{\text{far+near}}{2} \\
0 & 0 & 0 & 1 \\
\end{bmatrix} \\
&=
\begin{bmatrix}
\frac{2}{\text{right}-\text{left}} & 0 & 0 & -\frac{\text{right}+\text{left}}{\text{right}-\text{left}} \\
0 & \frac{2}{\text{top}-\text{bottom}} & 0 & -\frac{\text{top}+\text{bottom}}{\text{top}-\text{bottom}} \\
0 & 0 & -\frac{2}{\text{far}-\text{near}} & -\frac{\text{far}+\text{near}}{\text{far}-\text{near}} \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\end{aligned}
kde:
Cobrací osu Z, kvůli přechodu z right-handed do left-handed (týká se OpenGL 2),Sdefinuje velikost kvádru, který se vleze do clip space,Tposouvá počátek doprostřed kvádru.
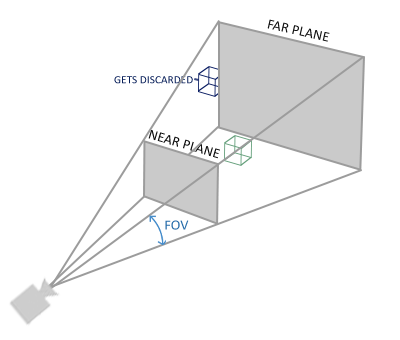
Perspektivní projekce
Zmenšuje objekty, které jsou dále od kamery. 1
Je definována 4 parametry:
\text{FOV}_y- field of view (úhel zorného pole) v ose Y,\text{aspect}- poměr šířky a výšky okna,\text{near}- blízká hranice,\text{far}- daleká hranice.
V matici P_\text{persp} se vyskytují následující mezihodnoty:
-
\text{top} = \text{near} \cdot \tan \left( \frac{\text{FOV}_y}{2} \right), -
\text{bottom} = -\text{top}, -
\text{right} = \text{top} \cdot \text{aspect}, -
\text{left} = -\text{right}. -
Translace frustumu Posouváme špičku frustumu do počátku souřadného systému. 3
T = \begin{bmatrix} 1 & 0 & 0 & -\frac{\text{left} + \text{right}}{2} \\ 0 & 1 & 0 & -\frac{\text{bottom} + \text{top}}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}Note
Všimni si, že. Pokud používáme 4-parametrickou verzi, tak je to matice identity a tím pádem není potřeba.
-
Perspective divide Objekty blíže k rovině
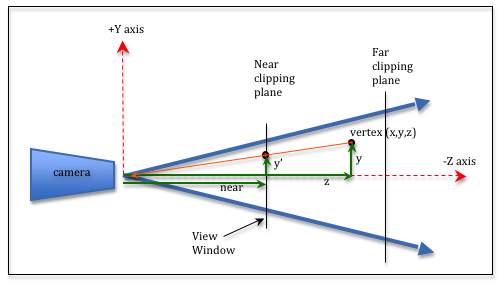
\text{near}budou větší než objekty dále. Rovina\text{near}reprezentuje plochu obrazovky, na kterou jsou všechny body promítány.Perspective divide 3
V obrázku výše je bod
(x, y, z)promítnut na rovinu\text{near}jako(x', y', near). Vznikají tak dva trojúhelníky, které jsou si sobě podobné a proto mají stejné poměry stran. Platí tedy\frac{y'}{\text{near}} = \frac{y}{z}. Paky' = \frac{y \cdot \text{near}}{z}. Chceme tedy, aby platilo:\begin{aligned} x' = \frac{x \cdot \text{near}}{z} \\ y' = \frac{y \cdot \text{near}}{z} \end{aligned}Což můžeme vyjádřit v homogenních souřadnicích vyjadřít dělením
wjako:D = \begin{bmatrix} \text{near} & 0 & 0 & 0 \\ 0 & \text{near} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & \color{red}{-1} & \color{red}{0} \\ \end{bmatrix} -
Velikost okna Šířka a výška okna dána pomocí
\text{left}, \text{right}, \text{bottom}, \text{top}se musí vlézt do intervalu(-1.0, 1.0), proto je potřeba provést škálování:S = \begin{bmatrix} \frac{2}{\text{right} - \text{left}} & 0 & 0 & 0 \\ 0 & \frac{2}{\text{top} - \text{bottom}} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} -
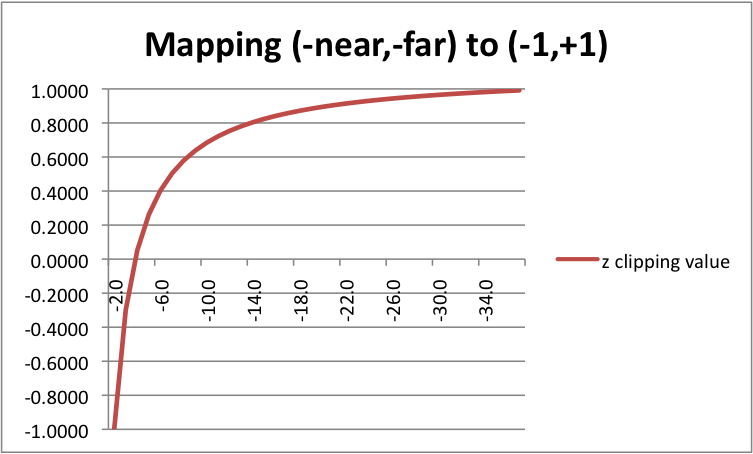
Přemapování hloubky Chceme zachovat tu schopnost souřadnice
znám říct, že něco je před něčím jiným. Potřebujeme proto přemapovat interval(-\text{near}, -\text{far})na(-1.0, 1.0). Jelikož desetinná čísla mají tendenci vytvářet artefakty, chceme aby toto mapování bylo nelineární tak, aby bylo přesnější blíže\text{near}. Použijeme\frac{c_1}{-z} + c_2, kdec_1ac_2jsou konstanty zvoleny pomocí:Note
Interval
(-\text{near}, -\text{far})obsahuje negace, neboť kamera se dívá do -Z osy, ale tyto hodnoty zadáváme jako kladná čísla.Note
-zv rovnici výše je zodpovědné za přepnutí mezi right-handed a left-handed systémem souřadnic v OpenGL.Depth mapping 3
\begin{aligned} -1.0 &= \frac{c_1}{-(-\text{near})} + c_2 \\ 1.0 &= \frac{c_1}{-(-\text{far})} + c_2 \end{aligned}Tedy:
\begin{aligned} c_1 &= \frac{2 \cdot \text{far} \cdot \text{near}}{\text{near} - \text{far}} \\ c_2 &= \frac{\text{far} + \text{near}}{\text{far} - \text{near}} \end{aligned}Pokud
\frac{c_1}{-z} + c_2přepíšeme jako\frac{(c_1 + c_2 \cdot (-z))}{-z} = \frac{(-c_2 \cdot z + c_1)}{-z}, můžeme opět použít homogenní souřadnice a děleníwa získáme:M_\text{depth} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -c_2 & c_1 \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -\frac{\text{far} + \text{near}}{\text{far} - \text{near}} & \frac{2 \cdot \text{far} \cdot \text{near}}{\text{near} - \text{far}} \\ 0 & 0 & -1 & 0 \\ \end{bmatrix}
Výsledná matice je:
P_\text{persp} = M_\text{depth} \cdot S \cdot D \cdot T =
\begin{bmatrix}
\textcolor{green}{\frac{2 \cdot \text{near}}{\text{right} - \text{left}}}
& 0
& 0
& \textcolor{purple}{-\text{near} \cdot \frac{\text{right} + \text{left}}{\text{right} - \text{left}}} \\
0
& \textcolor{blue}{\frac{2 \cdot \text{near}}{\text{top} - \text{bottom}}}
& 0
& \textcolor{#F56FA1}{-\text{near} \cdot \frac{\text{top} + \text{bottom}}{\text{top} - \text{bottom}}} \\
% Nika: použij cyklamenovou farbu
0
& 0
& -\frac{\text{far} + \text{near}}{\text{far} - \text{near}}
& \frac{2 \cdot \text{far} \cdot \text{near}}{\text{near} - \text{far}} \\
0 & 0 & -1 & 0 \\
\end{bmatrix}
Tahle matice funguje pro obecné frustum dané parametry \text{left}, \text{right}, \text{bottom}, \text{top}, \text{near}, \text{far}. Pokud dosadíme původní parametry za mezihodnoty:
\begin{aligned}
\textcolor{green}{\frac{2 \cdot \text{near}}{\text{right} - \text{left}}}
&= \frac{\textcolor{red}{2} \cdot \text{near}}{\textcolor{red}{2} \cdot \text{right}}
= \frac{\text{near}}{\text{top} \cdot \text{aspect}}
= \frac{\textcolor{red}{\text{near}}}{\textcolor{red}{\text{near}} \cdot \tan \left( \frac{\text{FOV}_y}{2} \right) \cdot \text{aspect}}
= \textcolor{green}{\frac{\cot \left( \frac{\text{FOV}_y}{2} \right)}{\text{aspect}}} \\
\textcolor{blue}{\frac{2 \cdot \text{near}}{\text{top} - \text{bottom}}}
&= \frac{\textcolor{red}{2} \cdot \text{near}}{\textcolor{red}{2} \cdot \text{top}}
= \frac{\textcolor{red}{\text{near}}}{\textcolor{red}{\text{near}} \cdot \tan \left( \frac{\text{FOV}_y}{2} \right)}
= \textcolor{blue}{\cot \left( \frac{\text{FOV}_y}{2} \right)} \\
\textcolor{purple}{-\text{near} \cdot \frac{\text{right} + \text{left}}{\text{right} - \text{left}}}
&= -\text{near} \cdot \frac{\color{red} \text{right} - \text{right}}{2 \cdot \text{right}}
= \textcolor{purple}{0} \\
\textcolor{#F56FA1}{-\text{near} \cdot \frac{\text{top} + \text{bottom}}{\text{top} - \text{bottom}}}
&= -\text{near} \cdot \frac{\color{red} \text{top} - \text{top}}{2 \cdot \text{top}}
= \textcolor{#F56FA1}{0}
\end{aligned}
dostaneme matici, na kterou se trochu lépe kouká: 4
P_\text{persp} = \begin{bmatrix}
\textcolor{green}{\frac{\cot \left( \frac{\text{FOV}_y}{2} \right)}{\text{aspect}}}
& 0
& 0
& \textcolor{purple}{0} \\
0
& \textcolor{blue}{\cot \left( \frac{\text{FOV}_y}{2} \right)}
& 0
& \textcolor{#F56FA1}{0} \\
0
& 0
& -\frac{\text{far} + \text{near}}{\text{far} - \text{near}}
& \frac{2 \cdot \text{far} \cdot \text{near}}{\text{near} - \text{far}} \\
0 & 0 & -1 & 0 \\
\end{bmatrix}
Základní afinní transformace
Opakování z Lineární algebry II:
-
Afinní prostor $\mathcal{A}$
Trojice(A, V, \oplus), kdeAje množina bodů,Vje vektorový prostor (zaměření) a\oplusje binární funkce\oplus : A \times V \to A. -
Standardní afinní prostor $\mathcal{A}_n$
Je afinní prostor(\mathbb{R}^n, \mathbb{R}^n, +). -
Afinní kombinace bodů
Výrazy tvarut_0 \cdot a_0 + t_1 \cdot a_1 + ... + t_n \cdot a_n, kdet_i \in \mathbb{R}, a_i \in \mathcal{A}a\sum_{i=0}^n t_i = 1. -
Afinní zobrazení
Zobrazeníf : \mathcal{A} \to \mathcal{A}, které zachovává afinní kombinace bodů.Složení nějakého lineárního zobrazení a translace.
-
Translace $T$
Pro posun v 2D prostoru podél osy(x, y):T = \begin{bmatrix} 1 & 0 & x \\ 0 & 1 & y \\ 0 & 0 & 1 \end{bmatrix}Pro posun ve 3D prostoru podél osy
(x, y, z):T = \begin{bmatrix} 1 & 0 & 0 & x \\ 0 & 1 & 0 & y \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \end{bmatrix} -
Rotace $R$
Pro rotaci v 2D prostoru o úhel\theta:R = \begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}Pro rotaci ve 3D prostoru o úhel
\theta:-
Kolem osy
X:R = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta & 0 \\ 0 & \sin \theta & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} -
Kolem osy
Y:R = \begin{bmatrix} \cos \theta & 0 & \sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \theta & 0 & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} -
Kolem osy
Z:R = \begin{bmatrix} \cos \theta & -\sin \theta & 0 & 0 \\ \sin \theta & \cos \theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
-
-
Škálování / scale $S$ Pro škálování v 2D prostoru:
S = \begin{bmatrix} x & 0 & 0 \\ 0 & y & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}Pro škálování ve 3D prostoru:
S = \begin{bmatrix} x & 0 & 0 & 0 \\ 0 & y & 0 & 0 \\ 0 & 0 & z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} -
Zkosení / shear (asi taky
S) Pro zkosení v 2D prostoru vektorem(x, y):S = \begin{bmatrix} 1 & x & 0 \\ y & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}Pro zkosení ve 3D prostoru podél plochy
YZ:S = \begin{bmatrix} 1 & Y & Z & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}Podél plochy
XZ:S = \begin{bmatrix} 1 & 0 & 0 & 0 \\ X & 1 & Z & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}Podél plochy
XY:S = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ X & Y & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}