21 KiB
| title | description |
|---|---|
| Grafy a grafové algoritmy | TODO |
Note
Reprezentace grafů. Souvislost grafu, rovinné grafy. Prohledávání grafu do šířky a do hloubky, nejkratší vzdálenosti, kostry, toky v sítích. Algoritmy: Bellman-Ford, Dijkstra, Ford-Fulkerson, Push-Relabel, maximální párování v bipartitních grafech.
IB000, IB002, IV003
Tip
Tahle otázka má solidní překryv s bakalářskými otázkami Grafy a Grafové problémy.
Terminologie
-
Graf
DvojiceG = (V, E)kde:Vje množina vrcholů;\lvert V \rvert = n,Eje množina hran;\lvert E \rvert = m,- hrana
e \in Eje dvojice vrcholůe = (u, v).
-
Váha grafu
Váha grafu je součet vah hran grafuG.w(G) = \sum_{e \in E(G)} w(e) -
Bipartitní graf
Graf jehož vrcholy lze rozdělit do dvou disjunktních množin tak, že všechny hrany vedou z jedné množiny do druhé.Example of bipartite graph without cycles by Watchduck
-
(Silná) souvislost grafu / (strongly) connected graph
GrafGje souvislý, pokud pro každé dva vrcholyu, v \in V(G)existuje cesta zudov. -
Slabá souvislost grafu / weakly connected graph
GrafGje slabě souvislý, pokud je souvislý jeho podgrafG'vzniklý odebráním orientace hran.Je souvislý alespoň, pokud zapomeneme, že hrany mají směr?
-
Silně souvislá komponenta / strongly connected component
Silně souvislá komponenta grafuGje jeho maximální podgrafG'takový, že je silně souvislý. Jinými slovy pro každé dva vrcholyu, v \in V(G')existuje cesta zudov. -
Planární / rovinný graf
GrafGje planární, pokud se dá nakreslit do roviny tak, že se žádné dvě hrany nekříží.Platí v nich Eulerova formule:
\lvert V \rvert - \lvert E \rvert + \lvert F \rvert = 2Kde
\lvert F \rvertje počet stěn -- oblastí ohraničených hranami.Vrcholy planárního grafu lze vždy obarvit 4 barvami tak, že žádné dva sousední vrcholy nebudou mít stejnou barvu.
-
(Hranový) řez / (edge) cut
Množina hranC \subseteq E(G)taková, že po odebrání hranCse grafGrozpadne na více komponent --G' = (V, E \setminus C)není souvislý.Analogicky se definuje i vrcholový řez / vertex cut.
Reprezentace grafů
-
Seznam následníků / adjacency list
Pro každý vrcholv \in Vmáme seznam (např. dynamic array nebo linked list)N(v)jeho následníků.Zabírá
\Theta(\lvert V \rvert + \lvert E \rvert)paměti. -
Matice sousednosti / adjacency matrix
Máme matici velikosti\lvert V \rvert \times \lvert V \rvertkdeA_{u,v} = 1pokud existuje hrana meziuav, jinakA_{u,v} = 0.Dá se pěkně použít k uložení vah.
-
Matice incidence / incidence matrix
Máme matici velikosti\lvert V \rvert \times \lvert E \rvertkdeA_{u,e} = 1pokuduje vrcholem hranye, jinakA_{u,e} = 0.Dá se z ní pěkně určit stupeň vrcholu.
Prohledávání grafu
Prohlédávání do šířky / breadth-first search (BFS)
Od zadaného vrcholu navštíví nejprve vrcholy vzdálené 1 hranou, poté vrcholy vzdálené 2 hranami, atd.
- Prohledávání po "vrstvách".
- Je implementovaný pomocí fronty (queue / FIFO).
- Časová složitost je
\mathcal{O}(\lvert V \rvert + \lvert E \rvert).
def dfs(graph: List[List[bool]], stamps: List[int], vertex: int) -> None:
if stamps[vertex] == -1:
stamps[vertex] = 0
stamp = stamps[vertex]
for i in range(0, len(graph)):
if graph[vertex][i] and stamps[i] != -1:
stamps[i] = stamp + 1
dfs(graph, stamps, i)
Prohlédávání do hloubky / depth-first search (DFS)
Od zadaného vrcholu rekurzivně navštěvuje jeho nenavštívené následníky.
- Prohledání po "slepých uličkách".
- Vynořuje se teprve ve chvíli, kdy nemá kam dál (backtrackuje).
- Je implementovaný pomocí zásobníku (stack / LIFO).
- Časová složitost je
\mathcal{O}(\lvert V \rvert + \lvert E \rvert).
def bfs(graph: List[List[bool]], stamps: List[int], vertex: int) -> None:
stamp = 0
queue = deque()
queue.append(vertex)
while len(queue) > 0:
current = queue.popleft()
stamps[current] = stamp
stamp += 1
for i in range(0, len(graph)):
if graph[current][i] and stamps[i] == -1:
queue.append(i)
Nejkratší vzdálenosti
Problém nalezení buď nejkratší cesty mezi dvěma vrcholy nebo nejkratší cesty z jednoho vrcholu do všech ostatních.
- Relaxace hrany $(u, v)$
Zkrácení vzdálenosti k vrcholuvprůchodem přes vrcholu. Musí platitu\text{.distance} + w(u, v) < v\text{.distance}. Hrana(u, v)je v takovém případě napjatá.
Bellman-Fordův algoritmus
Hledá nejkratší cesty z jednoho vrcholu do všech ostatních.
- Využívá relaxaci hran.
- Funguje i na grafech se zápornými hranami.
- Má časovou složitost
\mathcal{O}(\lvert V \rvert \cdot \lvert E \rvert).
def bellmanford(graph: List[List[Tuple[int, int]]], s: int) \
-> Tuple[bool, List[int], List[int]]:
# graph is an adjacency list of tuples (dst, weight)
distance = [float('inf') for i in range(0, len(graph))]
distance[s] = 0
parent = [-1 for i in range(0, len(graph))]
# relax all edges |V| - 1 times
for _ in range(1, len(graph)):
for u in range(0, len(graph)):
for edge in graph[u]:
(v, w) = edge
if distance[u] + w < distance[v]:
distance[v] = distance[u] + w
parent[v] = u
# check for negative cycles
for u in range(0, len(graph)):
for edge in graph[u]:
(v, w) = edge
if distance[u] + w < distance[v]:
return (False, None, None)
return (True, distance, parent)
Dijkstrův algoritmus
Hledá nejkratší cesty z jednoho vrcholu do všech ostatních.
- Je podobný BFS, ale používá prioritní frontu.
- Funguje pouze na grafech bez záporných hran.
Tip
Složitost závisí na implementaci prioritní fronty. Je to
\Theta(V)insertů,\Theta(V)hledání nejmenšího prvku,\Theta(E)snížení priority.
Note
Implementace níže používá pole (resp. Pythoní
list), tedy složitost je\Theta(V^2), jelikož hledání minima je lineární.
def dijkstra(graph: List[List[Tuple[int, int]]], s: int) \
-> Tuple[List[int], List[int]]:
# graph is an adjacency list of tuples (dst, weight)
distance = [float('inf') for i in range(0, len(graph))]
distance[s] = 0
parent = [-1 for i in range(0, len(graph))]
queue = list(range(0, len(graph)))
while len(queue) > 0:
u = min(queue, lambda v: distance[v])
queue.remove(u)
for edge in graph[current]:
(v, w) = edge
if distance[u] + w < distance[v]:
distance[v] = distance[u] + w
parent[v] = u
return (distance, parent)
V binární haldě by to bylo \Theta(V \log V + E \log V) a ve Fibonacciho haldě \Theta(V \log V + E).
Dijkstrův algoritmus lze optimalizovat, pokud nás zajímá jen nejkratší cesta mezi dvěma konkrétními vrcholy:
-
Funkce vrátí výsledek, jakmile je cílový vrchol vytažen z fronty.
-
Můžeme hledat zároveň ze začátku a konce pomocí dvou front a skončit, jakmile se někde potkají.
-
Můžeme přidat potenciál -- dodatečnou heuristickou váhu.
Important
Téhle variantě se říká A* (A star). Věnuje se mu část otázky Umělá inteligence v počítačových hrách.
Kostry
-
Spanning tree / kostra
Kostra grafuG = (V, E)je podgrafT \sube Gtakový, žeV(T) = V(G)jeTje strom. -
Minimum spanning tree (MST) / minimální kostra
Je kostraMgrafuGs nejmenší možnou váhou. Tedy pro každou kostruTgrafuG:w(M) \le w(T) -
Fundamental cycle
Fundamental cycle je cyklusCv grafuGtakový, že odebráním libovolné hranye \in Czískáme kostru. -
Fundamental cutset / řez
Fundamental cutset je množina hranDv grafuGtaková, že přidáním libovolné hranye \in Dzískáme kostru. -
Red rule
Najdi cyklus bez červených hran, vyber v něm neobarvenou hranu s nejvyšší cenou a obarvi ji červeně. -
Blue rule
Najdi řez bez modrých hran, vyber v něm neobarvenou hranu s nejmenší cenou a obarvi ji modře. -
Greedy algoritmus
Nedeterministicky aplikuj red rule a blue rule, dokud to jde (stačín-1iterací). Modré hrany tvoří MST. -
Jarníkův / Primův algoritmus
Speciální případ greedy algoritmu, kdy aplikujeme pouze blue rule. Princip:- Vyber libovolný vrchol
va přidej ho do kostryS. - Opakuj
n-1krát:- Vyber hranu
es nejmenší cenou, která má právě jeden vrchol vS. - Přidej druhý vrchol
edoS.
- Vyber hranu
Složitost: použijeme binární haldu
- Inicializace (
\inftyjako cena hrany mezi prázdnou kostrou a každým vrcholem):\mathcal{O}( \lvert V \rvert ) - Odstranění minima z binární haldy pro každý vrchol ve
V:\mathcal{O}( \lvert V \rvert \log \lvert V \rvert ) - Procházení každé hrany z
Ea snižování ceny:\mathcal{O}( \lvert E \rvert \log \lvert V \rvert ) - Celková složitost:
\mathcal{O}( \lvert E \rvert \log \lvert V \rvert ) - S Fibonacciho haldou jde zlepšit na:
\mathcal{O}( \lvert E \rvert + \lvert V \rvert \log \lvert V \rvert )
- Vyber libovolný vrchol
-
Kruskalův algoritmus
Princip: Seřaď hrany podle ceny vzestupně. Postupně přidávej hrany do kostry, vynechej ty, které by vytvořily cyklus.- Seřad hrany podle ceny vzestupně.
- Použij union-find na udržování komponent grafu.
- Procházej hrany postupně. Pokud oba konce hrany patří do různých množin, přidej ji.
Je to speciální případ greedy algoritmu.
Složitost:
- Inicializace union-findu:
\mathcal{O}( \lvert V \rvert ) - Seřazení hran:
\mathcal{O}( \lvert E \rvert \log \lvert E \rvert ) - Pro každou hranu provádíme dvakrát
find(\mathcal{O}(\log \lvert V \rvert )) a eventuálněunion(\mathcal{O}(\log \lvert V \rvert )):\mathcal{O}( \lvert E \rvert \log \lvert V \rvert ) - Celková složitost:
\mathcal{O}( \lvert E \rvert \log \lvert V \rvert )
-
Borůvkův algoritmus
Je "paralelní". Buduje modré stromy ze všech vrcholů naráz.- Pro každý vrchol inicializuj modrý strom.
- Dokud nemáš jen jeden modrý strom, opakuj fázi:
- Pro každý modrý strom najdi nejlevnější odchozí hranu a přidej ji (propojíš tak dva stromy).
Je to speciální případ greedy algoritmu, který spamuje jen blue rule.
Složitost:
- Počet komponent v první fázi:
\lvert V \rvert. - V každé fázi se zmenší počet komponent na polovin. Tím pádem bude
\log \lvert V \rvertfází. - Každá fáze zabere
\mathcal{O}( \lvert E \rvert )času, protože procházíme všechny hrany. - Celková složitost:
\mathcal{O}( \lvert E \rvert \log \lvert V \rvert )
Tip
Kruskal sice taky buduje stromy na více místech najednou, ale není "paralelní", protože minimalita kostry spoléhá na to, že hrany jsou seřazené. Borůvka takový požadavek nemá, a proto je paralelizovatelnější.
Složitosti algoritmů
| Algoritmus | ||
|---|---|---|
| Časová složitost | Prostorová složitost | Jarník (Prim) s prioritní frontou |
\mathcal{O}(\lvert E \rvert \log \lvert V \rvert ) |
\mathcal{O}( \lvert V \rvert ) |
Jarník (Prim) s Fibonacciho haldou |
\mathcal{O}(\lvert E \rvert + \lvert V \rvert \log \lvert V \rvert ) |
\mathcal{O}( \lvert V \rvert ) |
Kruskal |
\mathcal{O}(\lvert E \rvert \log \lvert V \rvert ) |
\mathcal{O}( \lvert V \rvert ) |
Borůvka |
Toky v sítích
-
Síť toků / flow network
Je čtveřice(G, s, t, c), kde:G = (V, E)je orientovaný graf,s \in Vje zdroj / source,t \in Vje cíl / stok / sink;s \neq t,c: E \rightarrow \mathbb{R}^+je funkce udávající kapacitu hran.
-
Network flow / tok
Je funkcef: E \rightarrow \mathbb{R}^+, která splňuje:- podmínku kapacity:
(\forall e \in E)(f(e) \ge 0 \land f(e) \leq c(e))- tok hranou je nezáporný a nepřevyšuje povolennou kapacitu
- podmínku kontinuity:
(\forall v \in V \setminus \{s, t\})(\sum_{e \in \delta^+(v)} f(e) = \sum_{e \in \delta^-(v)} f(e))- tok do vrcholu je stejný jako tok z vrcholu
- podmínku kapacity:
-
Hodnota toku $f$
\lvert f \rvert = \sum_{(s, v) \in E} f(s, v) = \sum_{(w, t) \in E} f(w, t)
Ford-Fulkerson
-
Residual network
Síť, která vzniká, když je už část kapacity hrany využívána tokemf. Umožnuje algoritmům změnit přechozí rozhodnutí a získat využitou kapacitu zpět.Je to pětice
G_f = (V, E_f, s, t, c_f), kdeE_f = \{ e \in E : f(e) < c(e) \} \cup \{ e^R : f(e) > 0 \},- pokud
e = (u, v) \in E,e^R = (v, u), - stem:[ c_f(e) = \begin{cases} c(e) - f(e) & \text{ pokud } e \in E \ f(e) & \text{ pokud } e^R \in E \end{cases} ]
-
Augmenting path $P$
Jednoduchás \rightsquigarrow tcesta v residuální sítiG_f.Note
T.j. cesta která může jít i proti směru toku
f.Bottleneck kapacita je nejmenší kapacita hran v augmenting path
P.To krásné na augmenting cestách je, že pro flow
fa augmenting pathPv grafuG_f, existuje tokf'takový, že\text{val}(f') = \text{val}(f) + \text{bottleneck}(G_f, P). Nový tokf'lze získat takto:*Augment*(f, c, P) { delta = bottleneck(P) *foreach*(e in P) { *if*(e in E) { f[e] = f[e] + delta } *else* { f[reverse(e)] = f[reverse(e)] - delta } } *return* f } -
Algoritmus Ford-Fulkerson
Hledá maximální tok. Augmentuje cestu v residuální síti dokud to jde.f(e) = 0pro každoue \in E.- Najdi
s \rightsquigarrow tcestuPv reziduální sítiG_f. - Augmentuj tok podél
P. - Opakuj dokud se nezasekneš.
*Ford-Fulkerson*(G) { *foreach* (e in E) { f(e) = 0 } G_f = reziduální síť vzniklá z G vzhledem k toku f *while* (existuje s ~> t cesta v G_f) { f = Augment(f, c, P) Updatuj G_f } *return* f }
Push-Relabel
-
Pre-flow
Ne-tak-docela tok.Funkce
ftaková, že- platí kapacitní podmínka:
(\forall e \in E)(0 \le f(e) \le c(e)), - platí relaxováné zachování toku: stem:[ (\forall v \in V - { s, t })(\sum_{e \text{ do } v} f(e) \ge \sum_{e \text{ ven z } v} f(e)) ].
- platí kapacitní podmínka:
-
Overflowing vertex
Takový vertexv \in V - \{ s, t \}, do kterého více přitéká než odtéká.\sum_{e \text{ do } v} f(e) > \sum_{e \text{ ven z } v} f(e) -
Excess flow
To, co je v overflowing vertexu navíc.e_f(v) = \sum_{e \text{ do } v} f(e) - \sum_{e \text{ ven z } v} f(e) -
Height function
Funkceh : V \to \N_0. Řekneme, žehje kompatibilní s preflow $f$, právě když-
source:
h(s) = |V| = n, -
sink:
h(t) = 0, -
height difference:
(\forall (v, w) \in E_{G_f})(h(v) \le h(w) + 1).Note
Pokud mezi dvěma vrcholy
(v, w)v reziduální síti vede hrana, pak jevnejvýše o jednu úroveň výš nežw.
-
-
Push operace
Pro (reziduálně-grafovou) hranu(v, w)se pokusí přesunout excess flow zvdow, aniž by porušil (reziduální) kapacitu(v, w).// Assumptions: e_f[v] > 0, c_f( (v, w) > 0) > 0, h[v] > h[w] *Push*(f, h, v, w) { delta_f = min(e_f[v], c_f(v, w)) *if*( (v, w) in E) f[(v, w)] += delta_f *else* f[(w, v)] -= delta_f e_f[v] -= delta_f e_f[w] += delta_f } -
Relabel operace
Zvýší výškuh(v)natolik, aby neporušil kompatibilituhsf.// Assumptions: // - v is overflowing: e_f[v] > 0 // - all residual neighbors of v the same height or higher: // forall (v, w) in E_f: h[v] \<= h[w] *Relabel*(f, h, v) { h[v] = 1 + min(h[w] | (v, w) in E_f) } -
Algoritmus Push-Relabel (Goldberg-Tarjan)
Hledá maximální tok.Princip: Pokud je nějaký vrchol overflowing, tak ho pushni nebo relabeluj. Pokud ne, tak jsi našel maximální tok.
*Push-Relabel*(V, E, s, t, c) { // initialize preflow -- default values *for*(v in V) { h[v] = 0 // height function e_f[v] = 0 // excess flow } n = |V| h[s] = n *for*(e in E) { f[e] = 0 // (pre)flow } // initialize preflow -- saturate connections from s *for*( (s, v) in E) { f[(s, v)] = c(s, v) // preflow maxes out all capacity e_f[v] = c(s, v) // presume all of it excess e_f[s] -= c(s, v) // yes, it will be negative } // the juicy part *while*(_any vertex is overflowing_) { v = _an overflowing vertex_ (has e_f[v] > 0) *if*(v _has a neighbor_ w _in_ G_f _such that_ h(v) > h(w)) { *Push*(f, h, v, w) } else { *Relabel*(f, h, v) } } *return* f }Korektnost: V průběhu výpočtu platí:
- Výška vrcholu nikdy neklesá.
- Pre-flow a výšková funkce jsou kompatibilní.
Složitost:
- Nejvýše
2^nRelabelů. 2nmsaturujících Push.4n^2mnesaturujících Push.- Relabel i Push jsou v
\mathcal{O}(1). - Celkem:
O(n^2m).
Srovnání algoritmů Ford-Fulkerson a Push-Relabel
| Ford-Fulkerson | |
|---|---|
| Push-Relabel (Goldberg) | global character |
| local character | update flow along an augmenting path |
| update flow on edges | flow conservation |
Maximální párování v bipartitních grafech
-
Párování / matching
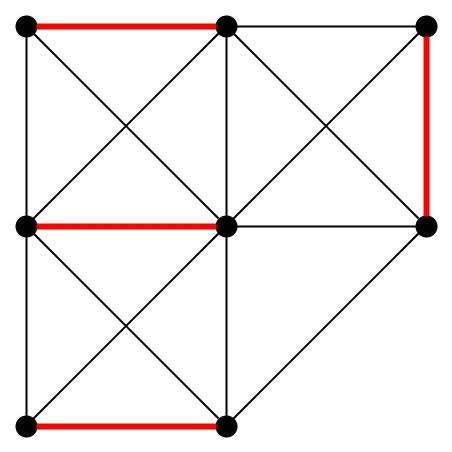
MnožinaM \sube Etaková, že žádné dvě hrany vMnemají společný vrchol. 1Prázdná množina je párováním na každém grafu. Graf bez hran má pouze prázdné párování.
Příklad párování, které je zároveň maximální by RRPPGG
-
Maximální párování
Takové párování, které má nejvyšší počet hran. Graf může mít několik maximálních párování. -
Perfektní párování
Takové párování, které páruje všechny vrcholy grafu. Každé perfektní párování je zároveň maximální. -
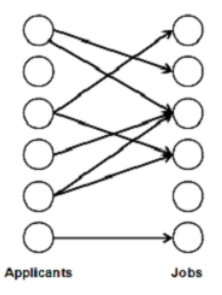
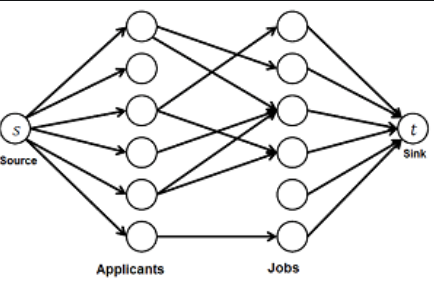
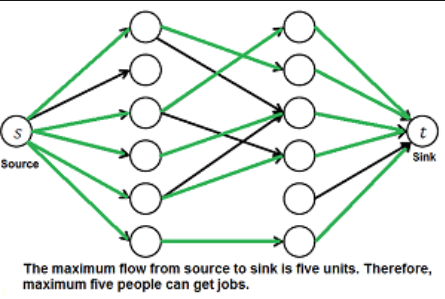
Maximum cardinality matching (MCM) v bipartitním grafu
Problém nalezení maximálního párování v grafu. Ve speciálním případě, kdy graf je bipartitní, se tento problém dá převést na problém nalezení maximálního toku v síti: 2