---
title: "Numerické metody"
description: "TODO"
---
> [!NOTE]
> Iterativní metody pro řešení nelineárních rovnic (Newtonova metoda a její modifikace). Přímé metody pro řešení systému lineárních rovnic (Gaussova eliminace, Jacobi, Gauss-Seidel, relaxační metody). Numerická diferenciace, diferenciační schémata.
>
> _MA018_
- **Numerická analýza / numerical analysis**\
Oblast matematiky / informatiky zabývající se tvorbou numerických metod a algoritmů, které řeší problémy matematické analýzy (např. derivace, integrály a podobný symbolický balast) pomocí numerické aproximace. [^numerical-analysis]
Je výhodná v situacích, kdy problém nelze řešit analyticky nebo je to příliš složité a není to (výpočetní) čas.
- **Notace chyb**
- $x$ je přesná hodnota,
- $\tilde{x}$ je aproximace $x$,
- $x - \tilde{x}$ je absolutní chyba $\tilde{x}$,
- $\lvert x - \tilde{x} \rvert \leq \alpha$ je odhad absolutní chyby,
- $\frac{x - \tilde{x}}{x}$ je relativní chyba,
- $\left\lvert \frac{x - \tilde{x}}{x} \right\rvert \leq \alpha$ je odhad relativní chyby.
- **Numerická stabilita**\
Schopnost numerické metody zpracovat chyby vstupních dat a výpočetních operací.
Desetinná čísla jsou v počítačích nevyhnutelně reprezentována nepřesně. Numericky stabilní metody jsou takové, které tyto nepřesnosti **nezhoršují**. [^numerical-stability]
- **Řád metody / order of accuracy / order of approximation**\
Hodnota reprezentující, jak rychle metoda konverguje k výsledku, resp. jak přesný je její odhad.
Numerická metoda obvykle konverguje snižováním nějakého _kroku_ $h$. Pokud ho lze zvolit libovolně malý, a lze-li prohlásit, že pro chybu aproximace $E$ platí: [^rate] [^numericka-metoda] [^order-question]
```math
\begin{aligned}
E(h) &\leq C \cdot h^p \\
E(h) &\in \mathcal{O}(h^p)
\end{aligned}
```
kde $C$ je konstanta. Pak $p$ je řád metody.
## Iterativní metody pro řešení nelineárních rovnic
- **Root-finding problem**\
Problém nalezení _kořenů_ (root) funkce $f$. T.j. takových parametrů $x, ...$, kde funkce vrací 0: [^root-finding]
```math
f(x, ...) = 0
```
- **Iterative methods for root-finding problem**\
Metody pro řešení root-finding problemu, které využívají iterativního přístupu. Tedy opakují nějaký výpočet a zpřesňují svůj odhad, dokud nedosáhnou požadované přesnosti. [^ma018] [^root-finding]
- **Řád metody / rate of convergence**\
Hodnota reprezentující, jak rychle metoda konverguje k výsledku. [^rate]
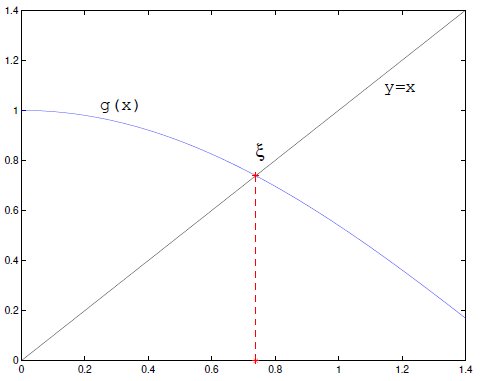
- **Prostá iterační metoda / metoda pevného bodu / fixed-point iteration**\
Používá se pro rovnice typu $x = g(x)$.
1. Zvolíme počáteční odhad $x_0$.
2. Opakujeme $x_{n+1} = g(x_n)$ dokud $\lvert x_{n+1} - x_n \rvert \leq \alpha$ (kde $\alpha$ je požadovaná přesnost).
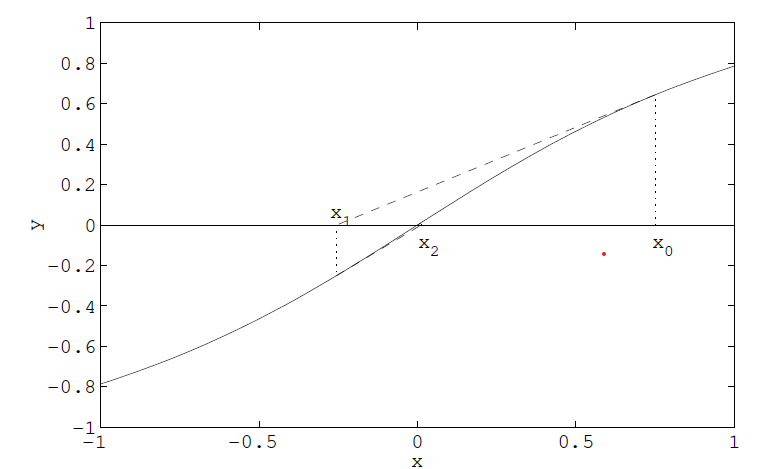
- **Newtonova metoda / metoda tečen**\
Používá k odhadu kořene funkce $f$ její tečnu v bodě $x_n$. Iterační funkce je:
```math
g(x_{k+1}) = x_k - \frac{f(x_k)}{f'(x_k)}
```
1. Zvolíme počáteční odhad $x_0$.
2. Další odhad je $x_{n+1} = g(x_n)$, tedy průsečík tečny fukce $f$ v bodě $x_n$ s osou $x$.
3. Opakujeme 2. dokud nedosáhneme požadované přesnosti odhadu.
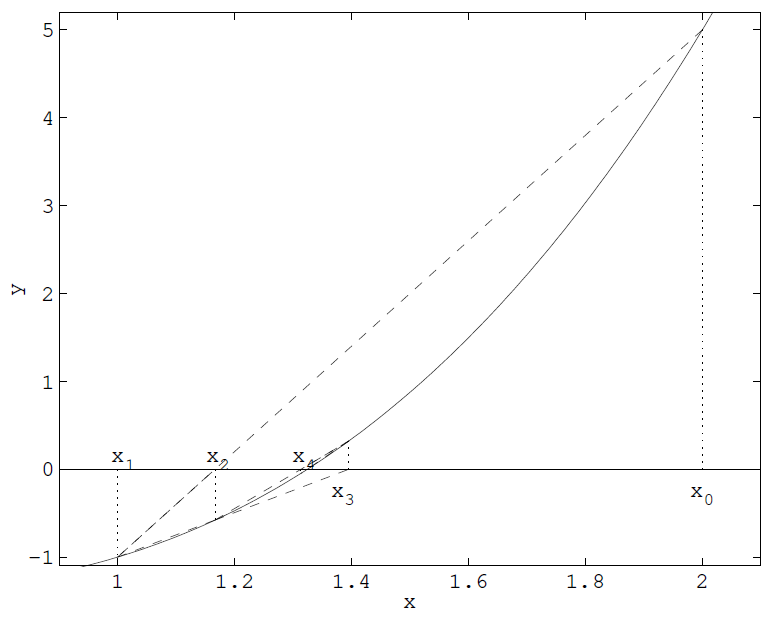
- **Metoda sečen / secant method**\
Používá k odhadu kořene funkce $f$ sečny, resp. _finite difference_, které aproximují derivaci funkce $f$. Díky tomu není potřeba znát derivaci funkce $f$. Iterační funkce je:
```math
g(x_{k+1}) = x_k - \frac{f(x_k)(x_k - x_{k-1})}{f(x_k) - f(x_{k-1})}
```
- **Metoda regula falsi**\
Je _bracketing_ metoda, tedy metoda, která využívá intervalu, ve kterém se nachází kořen. Nemusí se použít iterativně, ale v iterativní podobě tento interval postupně zmenšuje. [^regula-falsi]
```math
x_{k+1} = x_k - \frac{x_k - x_s}{f(x_k) - f(x_s)} f(x_k)
```
kde $s$ je největší index takový, že $f(x_k)f(x_s) < 0$.
## Přímé metody pro řešení systému lineárních rovnic
### Gaussova eliminace
Systém rovnice je přepsán do matice. Gaussova eliminace je posloupnost operací, jejichž cílem je převést matici do horní trojúhelníkové matice (_row echelon form_). [^gauss-elimination] Povoleny jsou následující operace:
- výměna dvou řádků,
- vynásobení řádku nenulovou konstantou,
- přičtení násobku jednoho řádku k jinému.
### Jacobiho iterační metoda
Iterativní algoritmus pro řešení soustavy lineárních rovnic. Rozděluje vstupní matici lineárních rovnic na matici diagonál $D$, dolní trojúhelníkovou matici $L$ a horní trojúhelníkovou matici $U$. [^jacobi-method]
Nechť $A\mathbf{x} = \mathbf{b}$ je systém $n$ lineárních rovnic. Tedy:
```math
A = \begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}, \qquad
\mathbf{x} = \begin{bmatrix}
x_{1} \\ x_2 \\ \vdots \\ x_n
\end{bmatrix} , \qquad
\mathbf{b} = \begin{bmatrix}
b_{1} \\ b_2 \\ \vdots \\ b_n
\end{bmatrix}.
```
Algoritmus vypadá takto:
1. Zvolíme počáteční odhad $\mathbf{x}^{(0)}$, nejčastěji $\vec{0}$.
2. Nový odhad získáme ze vztahu:
```math
\mathbf{x}^{(k+1)} = D^{-1}(\mathbf{b} - (L + U)\mathbf{x}^{(k)})
```
Jelikož $L + U = A - D$, dá to zapsat i jako:
```math
\mathbf{x}^{(k+1)} = D^{-1}\mathbf{b} + (I - D^{-1} A) \mathbf{x}^{(k)}
```
- **Spektrální poloměr**\
Spektrální poloměr $\rho$ matice $A$ je největší absolutní hodnota vlastního čísla matice $A$.
```math
\rho(A) = \max_{i=1,\ldots,n} |\lambda_i|
```
- **(Řádková) diagonální dominance**\
Matice $A$ je diagonálně dominantní, pokud platí:
```math
|a_{ii}| > \sum_{j=1, j \neq i}^n |a_{ij}|
```
Tedy absolutní hodnota prvku na diagonále je větší než součet absolutních hodnot všech ostatních prvků v řádku.
- _Striktní_: nerovnost je ostrá ($>$).
- _Slabá_: nerovnost je neostá ($\ge$).
Analogicky se definuje sloupcová diagonální dominance.
- **Konvergence Jacobiho metody**\
Jacobiho metoda konveguje pokud všechny následující podmínky:
1. Nechť $T_j = I - D^{-1} A$ je matice iterace Jacobiho metody. Pak Jacobiho metoda konverguje, pokud:
```math
\rho(T_j) < 1
```
2. Jacobiho metoda konverguje pro libovolný počáteční odhad $\mathbf{x}^{(0)}$, pokud $A$ je diagonálně dominantní (sloupcově nebo řádkově).
### Gaussova-Seidelova iterační metoda
Iterativní metoda pro řešení soustavy lineárních rovnic. Dělí vstupní matici na spodní trojúhelníkovou matici $L_*$ (včetně diagonály, tedy $L_* = D + L$) a striktně horní trojúhelníkovou matici $U$ (diagonála je nulová). Algoritmus vypadá takto: [^gauss-seidel]
1. Zvolíme počáteční odhad $\mathbf{x}^{(0)}$.
2. Nový odhad získáme ze vztahu:
```math
\mathbf{x}^{(k+1)} = L_*^{-1}(\mathbf{b} - U\mathbf{x}^{(k)}).
```
Alternativně:
```math
\begin{aligned}
T_{gs} &= (D + L)^{-1} U = L_*^{-1} U \\
\mathbf{x}^{(k+1)} &= T_{gs} \mathbf{x}^{(k)} + g,\quad g = L_*^{-1} \mathbf{b}
\end{aligned}
```
- **Konvergence Gaussovy-Seidelovy metody**\
Analogicky jako u Jacobiho metody, ale místo matice $T_j$ se použije matice $T_{gs} = (D + L)^{-1} U$.
### Relaxační iterativní metody
Modifikace Gauss-Seidelovy metody. Využívá parametr $\omega$, který určuje, jak moc se má nový odhad lišit od předchozího. Vztah pro další iteraci se mění na: [^relaxation-method]
```math
\begin{align*}
\mathbf{x}^{(k+1)} &= (D - \omega L)^{-1} [(1-\omega)D + \omega U]\mathbf{x}^{(k)} + \omega(D - \omega L)^{-1}\mathbf{b} \\
T_\omega &= (D - \omega L)^{-1} [(1-\omega)D + \omega U]
\end{align*}
```
- Pro $0 < \omega < 1$ se názývá metodou dolní relaxace. Je vhodná v případě, kdy Gauss-Seidel nekonverguje.
- Pro $\omega = 1$ je totožná s Gauss-Seidelem.
- Pro $\omega > 1$ se názývá metodou horní relaxace / SOR metodou. Zrychluje konvergenci Gauss-Seidela.
### Dekompozice matic
Metody podobné Gaussově eliminaci, ale s vlastnostmi, které mohou být vyhodné.
- **LU dekompozice**\
Rozdělení matice $A$ na horní dolní trojúhelníkovou matici $L$ a horní trojúhelníkovou matici $U$, tak že $A = LU$.
Je to v podstatě Gaussova eliminace. Matice $P$ je permutační matice, která prohazuje řádky:
```math
P \cdot A = L \cdot U
```
Platí, že:
```math
\begin{aligned}
A \cdot x &= b \\
A &= LU \\
LU \cdot x &= b
\end{aligned}
```
Původní problém řešení soustavy linárních rovnic se tedy převede na dva problémy:
```math
\begin{aligned}
y &= U \cdot x \\
L \cdot y &= b \\
\end{aligned}
```
Řešíme tedy dva systémy rovnic s trojúhelníkovými maticemi.
Oproti Gaussovi je výhodnější pro:
- Opakované řešení soustav s maticí $A$ a různými pravými stranami $b$.
- Inverzi matice $A$.
- Výpočet determinantu matice $A$.
- **QR dekompozice**\
Rozdělení matice $A$ na ortogonální matici $Q$ a horní trojúhelníkovou matici $R$ (už ne $U$), tak že $A = QR$.
```math
\begin{aligned}
A \cdot x &= b \\
A = QR \Rightarrow U \cdot x &= Q^T \cdot b \\
\end{aligned}
```
Protože je ortogonální a tedy $Q^{-1} = Q^T$.
Má lepší numerickou stabilitu než LU dekompozice.
## Numerická diferenciace
Algoritmy numerické diferenciace (derivace) počítají odhady derivace reálných funkcí -- aproximují $f'(x)$. Využívají při tom známé hodnoty této funkce a jiné znalosti a předpoklady. [^differentiation]
Numerická diferenciace se využívá pro aproximaci differenciálních rovnic (převodem na _diferenční rovnice_).
- **Langrangeova interpolace**\
Pokud známe hodnoty $f$ můžeme mezi nimi interpolovat pomocí Lagrangeova polynomu a derivovat ten, protože derivovat polynomy je jednoduché.
> [!IMPORTANT]
> Lagrangeovu interpolaci řeší část otázky [Křivky a povrchy](../szp05_krivky_a_povrchy/).
- **Finite difference method**\
Rodina metod numerické diferenciace, které využívají _konečné diference_. Tedy approximují limitu v definici derivace malými posuny ve vstupních hodnotách diferenciovaných funkcí. [^finite-difference-method]
Jednotlivým "odstínům" -- konkrétním výpočetním vzorcům -- téhle metody se říká _diferenciační schémata_.
> [!TIP]
> Abych pravdu řekl, nepodařilo se mi najít zdroj pro konkrétní definici pojmu "diferenciační schéma".
- **(Konečné) diference prvního řádu / first-order (finite) differences**\
Nejjednodušší schéma numerické diferenciace. Vychází z definice derivace. [^finite-difference]
- _Dopředná diference / forward (finite) difference_
```math
\frac{\partial f}{\partial x} \approx \frac{f(x+h) - f(x)}{h}
```
- _Zpětná diference / backward (finite) difference_
```math
\frac{\partial f}{\partial x} \approx \frac{f(x) - f(x-h)}{h}
```
- _Centrální diference / central (finite) difference_
```math
\frac{\partial f}{\partial x} \approx \frac{f(x+h) - f(x-h)}{2h}
```
kde $h$ je kladné číslo napodobující nekonečně malou změnu (limitu) v definici derivace. Může to být konstanta, může ale být i zvoleno adaptivně.
> [!TIP]
> Tečna je tak napodobena sečnou.
- **Richardson extrapolation**\
Způsob zlepšení rate of convergence iterativních metod. [^richardson]
[^ma018]: [MA018 Numerical Methods (podzim 2019)](https://is.muni.cz/auth/el/fi/podzim2019/MA018/)
[^numerical-analysis]: [Wikipedia: Numerical analysis](https://en.wikipedia.org/wiki/Numerical_analysis)
[^root-finding]: [Wikipedia: Root-finding algorithms](https://en.wikipedia.org/wiki/Root-finding_algorithms)
[^rate]: [Wikipedia: Rate of convergence](https://en.wikipedia.org/wiki/Rate_of_convergence)
[^regula-falsi]: [Wikipedia: Regula falsi](https://en.wikipedia.org/wiki/Regula_falsi)
[^gauss-elimination]: [Wikipedia: Gaussian elimination](https://en.wikipedia.org/wiki/Gaussian_elimination)
[^jacobi-method]: [Wikipedia: Jacobi method](https://en.wikipedia.org/wiki/Jacobi_method)
[^gauss-seidel]: [Wikipedia: Gauss-Seidel method](https://en.wikipedia.org/wiki/Gauss%E2%80%93Seidel_method)
[^relaxation-method]: [Wikipedia: Relaxation (iterative method)]()
[^differentiation]: [Wikipedia: Numerical differentiation](https://en.wikipedia.org/wiki/Numerical_differentiation)
[^finite-difference]: [Wikipedia: Finite difference](https://en.wikipedia.org/wiki/Finite_difference)
[^finite-difference-method]: [Wikipedia: Finite difference method](https://en.wikipedia.org/wiki/Finite_difference_method)
[^richardson]: [Wikipedia: Richardson extrapolation](https://en.wikipedia.org/wiki/Richardson_extrapolation)
[^linear-eq]: [Wikipedia: System of linear equations](https://en.wikipedia.org/wiki/System_of_linear_equations)
[^numerical-stability]: [Wikipedia: Numerical stability](https://en.wikipedia.org/wiki/Numerical_stability)
[^numericka-metoda]: [Wikipedia: Numerická metoda](https://cs.wikipedia.org/wiki/Numerick%C3%A1_metoda)
[^order-question]: [What is the intuitive meaning of order of accuracy and order of approximation?](https://math.stackexchange.com/questions/2873291/what-is-the-intuitive-meaning-of-order-of-accuracy-and-order-of-approximation)